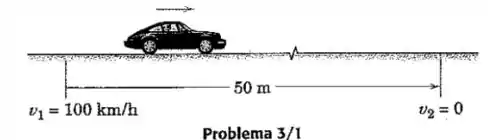
Durante um teste de frenagem, o carro com motor traseiro é parado a partir de uma velocidade inicial de em uma distância de . Se é sabido que todas as quatro rodas contribuem igualmente para a força de frenagem, determine a força de frenagem em cada roda. Suponha uma desaceleração constante para o carro de .

Qual é a força associada a essa aceleração? Vamos usar a segunda lei de Newton:

E agora supondo que a força é distribuída igualmente entre as quatro rodas, podemos dividir esse resultado para encontrar a força em cada uma:

E quando falamos em “força de frenagem” podemos tirar esse sinal negativo, porque o sentido da força já está implícito: