Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.10 - Ex. 247
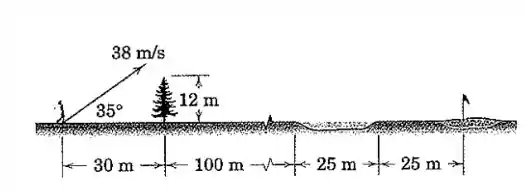
Logo após ter sido atingida por um taco, uma bola de golfe tem uma velocidade de direcionada a com a horizontal conforme apresentado. Determine a localização do ponto de impacto.
Passo 1
Bom, primeiro precisamos ver quanto tempo essa bola vai levar para voltar ao solo. Quem define esse tempo é a componente vertical da velocidade, porque é ela quem vai sofrer com a aceleração da gravidade puxando para baixo:
Vamos chamar de a altura inicial da bola, a questão é saber quanto tempo ela demora para voltar à mesma altura :
Passo 2
Agora teoricamente podemos simplesmente ver qual é a distância horizontal que a bola alcança nesse intervalo de tempo:
Beleza, a gente poderia encerrar a questão aqui, porque olhando na figura isso quer dizer que a bola cai na poça d’água, que fica nesse intervalo:
Mas precisamos ter certeza de que a bola não bate naquela árvore de metros de altura!
Passo 3
Vamos lá, quanto tempo demora para a bola estar na mesma posição da árvore no eixo horizontal? Bom, considerando que ela está a de distância:
E agora é só ver qual é a altura da bola nesse instante:
Ou seja, a bola passa por cima da árvore tranquilamente, e vai aterrisar na poça mesmo!
Resposta
O ponto de impacto fica na poça d’água.