Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.4 - Ex. 2
O caixote de está parado quando a força é aplicada. Determine a aceleração resultante do caixote se (a) , (b) e (c) .
Passo 1
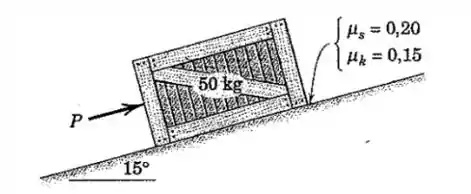
Vamos começar pensando nas forças que atuam sobre o caixote.
Empurrando o bloco ladeira abaixo nós temos a componente do peso:
E tentando balancear o peso temos a força de atrito e a força , então a soma das forças é:
Considerando o sentido positivo como sendo para cima do plano.
A força de atrito estático é a força mínima que deve ser feita para o bloco entrar em movimento, podemos calcular essa valor assim:
Já que a força normal tem que ser igual à componente do peso que fica perpendicular ao plano.
Passo 2
(a) No caso em que a força a força de atrito estático sozinha não é suficiente para “segurar” o peso, então o bloco entra em movimento, e então precisaremos usar o coeficiente de atrito cinético:
E então a aceleração do bloco pode ser calculada com a segunda lei de Newton:
E o sinal negativo indica que o movimento é ladeira abaixo.
´Vamos seguir essa mesma lógica nas próximas beleza? Verificar se existe movimento comparando o peso com o atrito estático, e caso tenha vamos calcular a aceleração com o atrito cinético.
Passo 3
(b) No caso em que a força empurra o bloco para cima, ainda temos o peso puxando o bloco para baixo:
Mas o atrito estático (a força mínima para gerar movimento) é , ou seja, não existe movimento, então:
Passo 4
(c) Quando a força é empurra o bloco para cima, o peso puxa o bloco para baixo e gera uma “resultante” , que é maior do que a força de atrito estático:
Ou seja, existe movimento ladeira acima! Agora vamos calcular a aceleração usando o atrito cinético, que agora vai estar no sentido de descer, já que ele é sempre contrário ao movimento:
E agora usando a segunda lei de Newton:
Pronto, resolvido!
Resposta
(a)
(b)
(c)