Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 3.Problemas - Ex. 50

Sabendo-se que um torque T de 2,3   k N m é aplicado ao cilindro E do Prob. 3.49, determinar (a) a máxima tensão de cisalhamento na barra cilíndrica AB; (b) a máxima tensão de cisalhamento no tubo CD

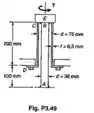
Passo 1

O desenvolvimento dessa questão é praticamente todo igual à questão anterior

Como toda questão de torção, a melhor forma de começar é calculando o momento de inércia.

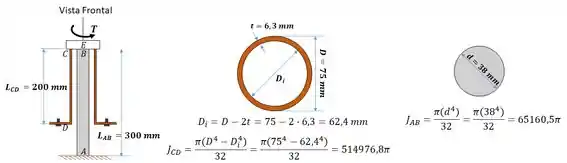
Passo 2

Para examinar melhor, vamos fazer uma seção e separar o tubo da barra:

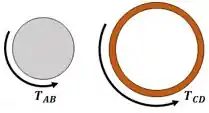
Como é uma situação estática, podemos afirmar que:

T = T A B + T C D

Como já temos o valor do torque:

2,3 = T A B + T C D

Mas ainda não temos todas as informações necessárias para calcular os torques. Então a gente tem que pensar em uma nova forma de relacionar os torques.

O tubo e a barra estão presos no ponto E. Isso quer dizer que tanto a barra quanto o tubo terão o mesmo ângulo de torção ϕ . A gente pode utilizar a equação do ângulo de torção para relacionar os torques.

Primeiro a gente monta as equações:

T o r ç ã o   n a   b a r r a   A B T o r ç ã o   n o   t u b o   C D ϕ A B = T A B L A B J A B G A B ϕ C D = T C D L C D J C D G C D

E a gente pode igualar:

ϕ A B = ϕ C D

T A B L A B J A B G A B = T C D L C D J C D G C D

Isolamos T A B :

T A B = T C D L C D J C D G C D ⋅ J A B G A B L A B

E aplicamos os valores:

T A B = T C D 200   m m 514976,8 π ⋅ 39 G P a ⋅ 65160,5 π ⋅ 77   G P a 300   m m

T A B = 0,167 ⋅ T C D

Passo 3

Agora temos o seguinte sistema:

2,3 = T A B + T C D T A B = 0,167 ⋅ T C D

Vamos resolvemos T C D :

2,3 = T A B + T C D

2,3 = 0,167 ⋅ T C D + T C D

T C D = 1,971   k N m

E resolvemos T A B

T A B = 0,167 ⋅ T C D

T A B = 0,329   k N m

Passo 4

Agora tá tranquilo. Basta aplicar a equação da tensão:

Para a barra AB:

τ A B = T A B c A B J A B

τ A B = 0,329   k N m ⋅ 38   m m 2 65160,5 π   m m 4

τ A B = 30,54   M P a

Para o tubo CD:

τ C D = T C D c C D J C D

τ C D = 1,971   k N m ⋅ 75   m m 2 514976,8 π   m m 4

τ C D = 45,69   M P a

Resposta

  1. τ A B = 30,54   M P a
  2. τ B C = 45,69   M P a
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A barra circular de seção cheia AB é feita de aço elastiplástico com T E = 151,7M P aeG = 77,2G P a . Sabendo que um torque T = 8473k N * m m é aplicado à barra e depois removido, determine a tensão d
Um eixo sólido de seção circular com 18m m de diâmetro é feito de um material considerado elastoplástico com t y =145M P a e G = 77,2G P a . Para um eixo com 1,2 m de comprimento, determine a máxima t
Uma barra circular cheia é feita de um material considerado elastoplástico chamado de T E e ϕ E ⋅ respectivamente,o torque se o ângulo de torção no início do escoamento, determine o ângulo de torção f
O eixo A B é feito de um material elastoplástico com T E =90M P a e G = 30G P a .Para o carregamento mostrado , determine (a) o raio do núcleo elástico da seção transversal do eixo e (b) o ângulo de t
Um eixo de seção vazada tem 0,9 m de comprimento e a seção transversal mostrada. O aço é considerado elastoplástico com τ E = 180M P a e G = 77,2 G P a . Determine a o ângulo de torção quando a seção