Uma placa anelar de espessura t e módulo de elasticidade transversal G é usada para conectar o Eixo AB de raio ao tubo CD de raio interno . Sabendo-se que o torque T é aplicado à extremidade A do eixo AB e que a extremidade D do eixo CD é engastada (a) determinar a intensidade e a localização da máxima tensão de cisalhamento na placa anelas; (b) mostrar que o ângulo de rotação da extremidade B do eixo em relação à extremidade C do tubo é:

Abaixo a gente tem um desenho da estrutura.

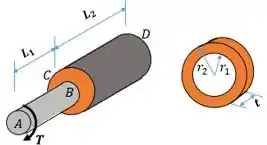
Como a placa anelar é muito fina, uma análise normal dos torques não será suficiente.

Então é o seguinte, vamos olhar melhor a placar:

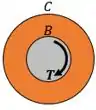
E como vamos avaliar o torque na placa? Para isso vamos usar um pouco de matemágica

Vamos olhar novamente para a nossa seção. Agora vamos imaginar um raio qualquer e uma região pontilhada formada por esse raio:

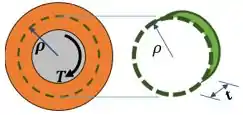
Nessa região pontilhada, a tensão de cisalhamento é .

Agora vamos considerando a área do contorno (destacada em verde)

Por definição, tensão é força sobre área. Então podemos determinar uma força equivalente que é aplicada na região lateral, que é capaz de gerar está tensão de cisalhamento.

Se a gente der uma olhada no diagrama de corpo livre da região pontilhada vamos ver que:

Para essa região ser estática, então a força tem que compensar o torque :

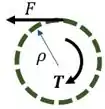
Vamos fazer o somatório de torques:

Vamos expandir:

E agora podemos isolar a tensão em função do raio qualquer