Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.4 - Ex. 86
O eixo, alavanca e manopla estão soldados e formam um único corpo rígido. Sua massa combinada é de , com centro de massa em . O conjunto está montado sobre os mancais e e qualquer giro é evitado pela haste . Determineas forças exercidas sobre o eixo pelos mancais e quando o momento de é aplicado à manopla, como mostrado. Essas forças variaria se o momento fosse aplicado ao eixo em vez de sê-lo na manopla?
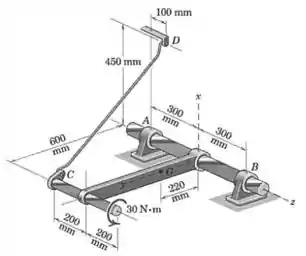
Passo 1
Esse é um problema bastante difícil de resolver na forma tridimensional. É uma boa analisar cada plano separadamente.
Começamos com uma vista “de lado”, no plano :
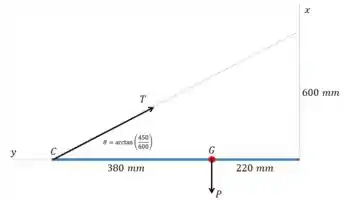
Podemos usar uma equação de equilíbrio nesse plano para encontrar o módulo de . Vamos calcular o momento em relação ao eixo , que passa pela extremidade direita da barra, saindo do plano da página.
E o último termo é o momento de que está representado no desenho do enunciado, e é em torno do eixo :
Passo 2
Agora vamos analisar o plano :
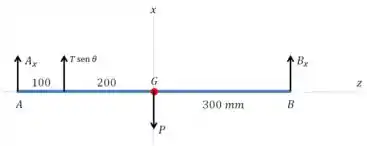
Vamos calcular o momento em relação ao ponto :
E podemos aproveitar esse resultado para calcular usando a condição de equilíbrio para as forças:
Passo 3
E por último vamos analisar o plano (vista “de cima”):
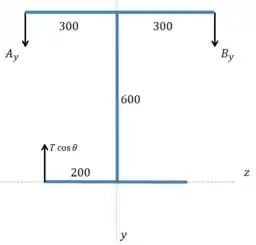
E agora vamos considerar o momento em relação ao ponto onde a força é aplicada:
E agora podemos usar a condição de equilíbrio das forças para encontrar :
Passo 4
Agora já podemos calcular os módulos das forças:
E a última pergunta é: as forças variam se o momento de fosse aplicado ao eixo ? E aqui só precisamos lembrar de um princípio importante: um mesmo binário pode ser aplicado em qualquer ponto no corpo sem gerar nenhuma alteração no sistema.
Para que houvesse alguma diferença, seria preciso alterar a “direção” (rotacionar) o binário.
Resposta
Os módulos são e . As forças não variariam se o momento fosse aplicado em .