Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.3 - Ex. 51
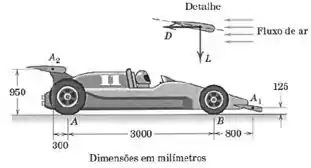
O carro completo, com seu motorista, tem massa de e, sem os dois aerofólios, tem uma distribuição de peso igual entre a dianteira e a traseira em uma dada velocidade na qual o carro não sofre empuxo para cima. Estima-se que nessa velocidade cada um dos aerofólios e , vai gerar de força direcionada para baixo, , e de força de arraste sobre o carro. Especifique, nessa velocidade, as reações verticais e sob os dois pares de rodas quando os aerofólios forem colocados. Considere que a colocação dos aerofólios não afeta as condições de arraste e de empuxo para cima no carro e que o motor tem potência suficiente para manter o equilíbrio nessa velocidade. O peso do aerofólio pode ser desprezado.
Passo 1
Quando estamos sem os aerofólios, as reações verticais e respondem apenas ao peso do carro:
O enunciado diz que quando adicionarmos esses aerofólios (na traseira e na dianteira) teremos forças de na vertical em cada um, e então:
Porque as forças normais vão passar a ter que suportar, além do peso, essas forças geradas pelos aerofólios.
Beleza, essa é nossa primeira equação.
Passo 2
Agora vamos fazer a mesma análise em relação ao momento. Mais uma vez, vamos considerar apenas a variação nas forças normais após a inclusão dos aerofólios.
Começamos calculando o momento gerado pelas forças horizontais nos aerofólios. Para que uma das variáveis desconhecidas suma da equação, vamos calcular esse momento em relação ao ponto :
E agora as forças verticais dos aerofólios:
E esse dois momentos tem que ser compensados pelos momentos das reações verticais:
E agora vamos aplicar a condição de equilíbrio:
Lembrando que e :
Passo 3
E agora podemos substituir isso na equação de cima:
E como essa é apenas a variação, temos que somar aos valores inicias para encontrar o resultado final:
Pronto!
Resposta
As reações normais são e .