Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 13.Problemas - Ex. 9
Cada uma das três chatas tem massa de Mg, ao passo que o rebocador tem massa de Mg. À medida que as chatas estão sendo puxadas para frente com uma velocidade constante de 4 m∕s, o rebocador deve superar a resistência do atrito da água, que é de kN para cada chata e kN para o rebocador. Se o cabo entre e se rompe, determine a aceleração do rebocador.
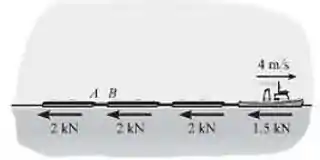
Passo 1
Analisando o problema, o rebocador está puxando as três chatas a uma velocidade constante de e então, o cabo localizado entre e se rompe e o rebocador mais as duas chatas restantes, adquirem uma aceleração que queremos determinar. No primeiro momento , precisamos determinar qual a força que o rebocador possui antes do rompimento do cabo. Do diagrama de corpo livre, temos:
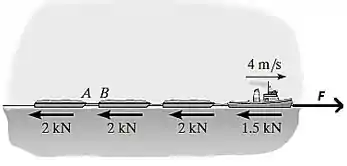
Como antes do rompimento do cabo, o corpo se movia com velocidade constante (, temos:
N
Passo 2
Agora que sabemos a força do rebocador, podemos aplicar a equação do movimento para determinarmos a aceleração do corpo depois do rompimento do cabo, então:
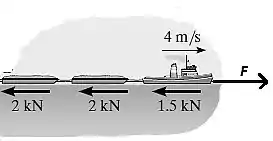
Passo 3
Substituindo os valores da força , das massas das duas chatas e do rebocador na equação acima, podemos determinar o seguinte valor da aceleração:
Resposta
A aceleração do rebocador será igual a 0,0278.