Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 13.Problemas - Ex. 30
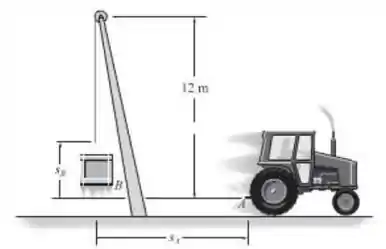
O trator é usado para içar a carga B de com o sistema de cordas de de comprimento, lança e polia. Se o trator se move para a direita com aceleração de e tem velocidade de no instante que , determine a tração na corda neste instante. Quando , .
Passo 1
Temos que ir com muita calma. Este problema é um pouco complicado no início. Mas só um pouco! Precisamos descobrir o valor da aceleração do bloco para que possamos calcular a tração a que ele está sujeito. Mas para isto, precisamos realizar o seguinte procedimento.
Precisamos escrever uma equação que envolva tudo que envolva o trator e suas derivadas), e que envolva também o nosso bloco e suas derivadas). A única forma que temos é ao escrevermos em função da nossa corda, que possui um comprimento finito de .
Passo 2
Ao carro se deslocar para a direita, conforme podemos ver pela figura da questão, a corda vai formar um triângulo retângulo, como podemos ver abaixo:
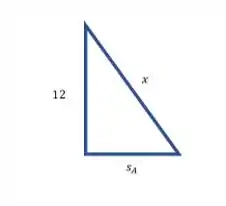
Cujo comprimento da sua hipotenusa é:
Agora, vamos relacionar este comprimento com todo a nossa corda. Sendo assim, temos a seguinte equação:
Em que o termo está relacionado a altura vertical da corda acima do bloco B. Como queremos determinar a aceleração do bloco , basta derivarmos esta função acima duas vezes!! Desta forma, temos:
Derivando mais uma vez, temos:
Portanto,
Passo 3
Agora que descobrimos o valor da aceleração do bloco B, temos que a tração no cabo é: