A caixa tem massa de kg e está sendo puxada por uma corrente que está sempre direcionada a da horizontal, como mostrado. Determine a aceleração da caixa em s se o coeficiente de atrito estático é, o coeficiente de atrito cinético é , e a força de reboque é , onde é dado em segundos.
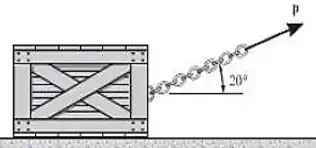
Passo 1
Inicialmente, iremos fazer uma breve análise do problema. Uma força que em 2 segundos possui um valor N é aplicada na caixa de . Em contra partida, uma força de resistência é desenvolvida devido ao atrito entre a caixa e o plano. A pergunda que devemos fazer é, será que a força é suficiente para mover o bloco? Podemos verificar através das equações de equilíbrio:

Isolando na equação acima, temos:
N
Isolando na equação acima, temos:
N
A força N é igual a força aplicada na caixa. Camparando com a força de atrito máxima entre a caixa e o plano, temos:
N N
Assim, concluímos que a força N moverá a caixa.
Passo 2
Agora, iremos determinar a aceleração da caixa através da equação do movimento. Do diagrama de corpo livre, temos:

Como não há movimento na direção y, temos:
Passo 3
Substituindo o valor da força normal e da massa na equação acima, chegaremos no seguinte valor para aceleração:
Resposta
A aceleração da caixa em s é igual a