Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 13.Problemas - Ex. 10
A caixa tem massa de kg e está sendo puxada por uma corrente que está sempre direcionada a da horizontal, como mostrado. Se a intensidade de é aumentada até a caixa começar a escorregar, determine a aceleração inicial da caixa se o coeficiente de atrito estático é e o coeficiente de atrito cinético é .
Passo 1
Podemos verificar que o bloco so se moverá se a força for suficiente para vencer a força resistiva , então o primeiro passo para solução do problema é determinar a força imediatamente antes da caixa começar a se mover. Do diagrama de corpo livre estático, temos:
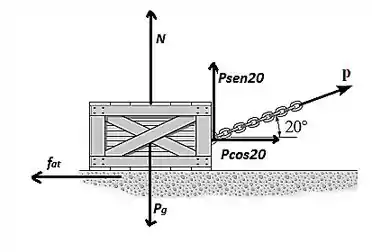
Como não há movimento do bloco na direção y, a equação acima fica:
Não havendo movimento na direção x, temos:
Por definição:
Então:
Passo 2
Do diagrama de corpo livre, determinamos as seguintes equações:
Resolvendo esse sistema de equações, chegaremos aos seguintes valores para força e normal :
N N
Passo 3
O terceiro e ultimo passo e determinar a aceleração inicial do bloco através da equação do movimento, assim:
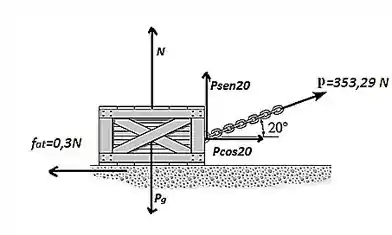
m
Como não há movimento do bloco na direção y, temos
N
Resposta
A aceleração inicial do bloco será igual a .