Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 13.Problemas - Ex. 12
Determine a aceleração do sistema e a tração em cada cabo. O plano inclinado é liso, e o coeficiente de atrito cinético entre a superfície horizontal e o bloco é
Passo 1
O primeiro passo é determinar a equação do movimento do bloco , e . Analisando o problema, percebemos que as acelerações dos blocos são iguais.
Do diagrama de corpo livre do bloco , temos::
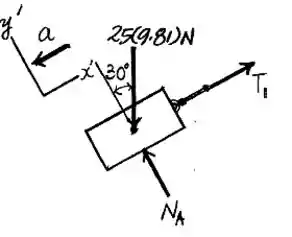
Do diagrama de corpo livre do bloco , temos:
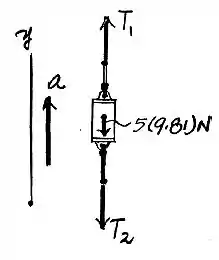
Do diagrama de corpo livre do bloco , temos:
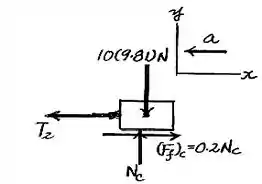
Passo 2
Das equações do movimento acima, chegamos as seguintes equações para os blocos , e :
(1)
(2)
(3)
Resolvendo esse sistema de equações, chegaremos aos seguintes valores para as trações e e a aceleração :
Resposta
a aceleração do sistema e a tração em cada cabo são iguais a:
Exercícios de Livros Relacionados
4/111) Substitua a corrente empilhada no Prob.4/92 por um rolo de corda de massa ρ por unidade de comprimento e comprimento total L como mostrado e determine a velocidade da seção em queda em termos d
A bola de 250g é suportada pelo jato vertical de água doce que escoa a partir do bocal com 12m m de diâmetro a uma velocidade de 10m / s . Calcule a altura h da bola acima do bocal. Suponha que o esco
O tubo curvo mostrado possui uma área de seção transversal A e está suportado em seu plano pela tração T aplicada a seus flanges pelos tubos adjacentes aos quais está conectado (não mostrados). Se a v
A pá com 90 ° se desloca para a esquerda com uma velocidade constante de 10m / s contra uma corrente de água doce escoando com uma velocidade de 20m / s a partir do bocal com 25m m de diâmetro. Calcul
O jet ski atinge sua velocidade máxima de 70k m / h quando operando em água salgada. A admissão de água é por uma passagem horizontal na parte inferior do casco, assim a água entra na admissão com a v