Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 3.Problemas - Ex. 98

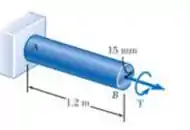
O eixo sólido mostrado é feito de um aço baixo carbono considerando elastoplástico com G = 77,2   G P a e t E = 145   M P a . determine o ângulo de giro produzido pela aplicação de um torque de intensidade (a) T = 600   N ⋅ m , (b) T = 1000 N ⋅ m .

Passo 1

E ai gurizada tudo belezinha? Espero que sim!! O enunciado pede que a gente determine o ângulo de giro produzido pela aplicação de um torque de intensidade (a) T = 600   N ⋅ m , (b) T = 1000 N ⋅ m ., então temos os seguintes dados:

c = 1 2 d = 15   m m = 15 × 10 - 3 m

Agora, vamos ver os cálculos do torque no início do escoamento:

τ = T c J = 2 T π c 3 T E = π c 3 τ Y 2 = π 15 × 10 - 3 3 145 × 10 6 2 = 768,71   N ⋅ m

  1. Considere o torque T = 600   N ⋅ m o eixo elástico é T ≤ T E . , então partiu calcular o ângulo :D

φ = T L G J = 2 T L π c 4 G = 2 600 1,2 π 15 × 10 - 3 4 77,2 × 10 9 = 0,11728   r a d

φ = 6 , 72 °

Passo 2

Para o torque de T = 1000 N ⋅ m   sendo que T > T E onde se desenvolve uma zona plástica, podemos calcular o ângulo a partir da equação de torque abaixo :D

T = 4 3 T E 1 - φ Y φ 3               φ Y φ = 4 - 3 T T E 3

Isolando o ângulo temos:

φ Y = T E L G J = 2 T E L π c 4 G = 2 768,71 2,1 π 15 × 10 - 3 4 77,2 × 10 9 = 0,15026   r a d

φ Y φ = 4 - 3 1000 768,71   3 = 0,46003

φ = φ 0,46003 = 0,15026 0,46003 = O , 32663

φ = 18,71 °

Resposta

  1. φ = 6,72 °
  2. φ = 18,71 ° .
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um torque T é aplicado como mostrado a um tronco de cone maciço AB. Mostrar por integração que o ângulo de torção em A é: ϕ A = 7 T L 12 π G c 4
Um eixo maciço e um eixo vazado são feitos de mesmo material e têm o mesmo peso e o mesmo comprimento. Expressando por n a reção c 1 / c 2 , mostrar que a relação T m / T v , entre o torque T m do eix
Resolver o Prob. 3,28,considerando que um furo de 25,4 mm foi broqueado ao longo do eixo.
A barra cilíndrica A B tem um diâmetro d s = 44,5m m e é feita de um aço com G = 77G P aeτ a d m = 83M P a , enquanto que o tubo C D é feito de um latão com G = 39G P a e τ a d m = 48,5M P a . Determi
Os torques mostrados são aplicados às polias A, B, C e D. Sabendo-se que todo o eixo é maciçi, tem 120 mm de comprimento e é feito de aço (G= 77 GPa), determinar o ângulo de torção entre (a) A e C; (b