Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 3.Problemas - Ex. 54
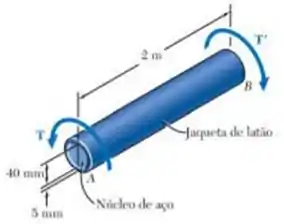
O eixo composto mostrado consiste em uma jaqueta de latão de 5.08 mm de espessura unido a um núcleo de aço de 40 mm de diâmetro . As tensões de cisalhamento do eixo admissíveis são: para o latão 20 MPa e para o aço, 45 MPa. Determine:
(a) o maior torque que pode ser aplicado ao eixo composto e
(b) o ângulo de rotação correspondente de B relativo a A.
Passo 1
Para um eixo de comprimento L e raio c, submetido a um momento torsor T, temos que o ângulo de torção é φ e a deformação de cisalhamento máxima é:
Mas pela Lei de Hooke:
Então igualando o segundo termo das duas expressões, temos que o ângulo de rotação é:
Substituindo na fórmula do torque, , temos:
Passo 2
Vamos calcular o torque máximo, com a expressão acima:
Para a jaqueta de latão temos:
Para o núcleo de aço:
Então o torque máximo é:
Passo 3
Agora para calcular o ângulo de rotação, temos, da fórmula do torque:
Para a jaqueta de latão:
Para o aço:
Nesse caso, a resposta é o menor ângulo encontrado.