Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 4.Problemas - Ex. 7

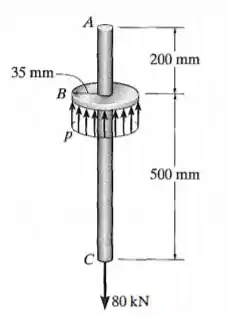
O eixo A C de aço A - 36 com 15   m m de diâmetro é sustentado por um colar rígido fixado ao eixo B . Se for submetido a uma carga axial de 80   k N em sua extremidade, determine a distribuição de pressão uniforme p no colar exigida para o equilíbrio. Calcule também o alongamento nos segmentos B C e B A .

Passo 1

Como o material tratado no problema é o aço A - 36 temos que o módulo de elasticidade é tabelado e dado por E = 200 G P a . O alongamento será dado pela seguinte fórmula

δ = P ⋅ L A ⋅ E

Onde L é a extensão do segmento que estamos analisando. Além disso, desejamos também calcular a distribuição de pressão uniforme que podemos encontrar através das equações de equilíbrio para o corpo.

Passo 2

Através da equação de equilíbrio das forças na direção y vamos obter

∑ F y = 0 → p ⋅ A c o l a r - P c = 0 → p = P c A c o l a r

Onde

A c o l a r = π 4 ⋅ [ 2 ⋅ 35 m m 2 - 15 m m ]

→ p = 80 k N π 4 ⋅ [ 2 ⋅ 35 m m 2 - 15 m m ] ≈ 21,79 M P a

Agora, vamos analisar sobre o alongamento. Tomemos o egmento A B e vamos observar que não tem nenhuma força na vertical de modo que

δ b a = 0

Já para o segmento B C nós temos

δ b c = P b c ⋅ L b c E ⋅ A = 80 k N ⋅ 500 m m 200 G P a ⋅ π 4 ⋅ 15 m m 2 ≈ 1,132   m m

Resposta

p = 21,79 M P a ,   δ b c = 1,132   m m   e   δ b a = 0 m m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O sistema articulado é composto por três elementos de aço A - 36 conectados por pinos, cada um com área de seção transversal de 500m m 2 . Se uma força vertical P=250k N for aplicada à extremidade B d
O raio do pedestal apresentado na figura é definido pela função r=2 / ( 2+y 1 2 )m , onde y é dado em metros. Se o módulo de elasticidade para o material for E=100M P a , determine o deslocamento da p
O poste é feito de abeto Douglas e tem diâmetro de 60m m . Se estiver sujeito a uma carga de 20k N e o solo proporcionar resistência ao atrito w=4k N / m uniformemente distribuída ao longo de seus lad
A viga rígida está apoiada em suas extremidades por dois tirantes de a ç oA - 36 ç . Os diâmetros das hastes são d A B=12m med c d=7,5m m . Se a tensão admissível para o aço for σ a d m=115M P a , det
Resolva o Problema 4.24 incluindo P e o peso do material e também considerando que o peso específico da haste é γ (peso por unidade de volume).