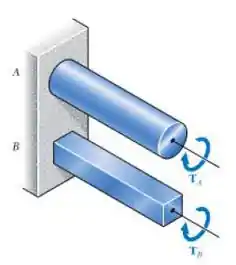
Os eixos A e B são feitos do mesmo material e têm mesmo comprimento e área de seção transversal, mas A tem seção transversal circular e B tem seção transversal quadrada. Determine a relação dos valores máximos dos ângulos pelos quais os eixos A e B, respectivamente, podem ser girados quando os dois eixos são submetidos ao mesmo torque . Assuma que ambas as deformações são elásticas.

E ai gurizada tudo belezinha? O enunciado pede que a gente Determine a relação dos valores máximos dos ângulos pelos quais os eixos A e B, respectivamente, podem ser girados quando os dois eixos são submetidos ao mesmo torque .

Considere que:

raio da seção do círculo lado da seção quadrada B.

Para áreas iguais,

Círculo:

Quadrado:

Da tabela 3.1, temos o valor de:

Razão:

Da