Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 2.Problemas - Ex. 21
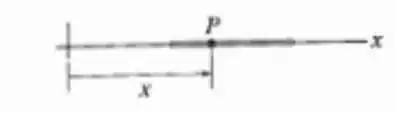
Um cabo fino que se encontra ao longo do eixo x é deformado de tal modo que cada um de seus pontos sofre um deslocamento ao longo do eixo. Se k for constante, qual a deformação normal em qualquer ponto P ao longo do cabo?
Passo 1
Sabemos que a deformação é a derivada do deslocamento, logo:
Resposta
Exercícios de Livros Relacionados
Use a lei de Hooke, Equação 10.18, para desenvolver as equações de transformação da deformação, equações 10.5 e 10.6, a partir das equações de transformação de tensão, 9.1 e 9.2.
A roseta de deformação a 60° está montada sobre uma viga. As seguintes leituras foram obtidas para cada extensômero: ∈ a = - 780 × 10 - 6 ;∈ b = 400 × 10 - 6 e ∈ c = 500 × 10 - 6 . Determine (a) as de
A roseta de deformação a 45 ° está montada sobre um eixo de aço. As seguintes leituras foram obtidas em cada extensômetro: ϵ a = 800 ( 10 - 6 ) , ϵ b = 520 ( 10 - 6 ) , ϵ c = - 450 ( 10 - 6 ) . Determ
A roseta de deformação a 45° está montada próxima ao dente da ferramenta. As seguintes leituras foram obtidas para cada extensômero: ∈ a = 800 × 10 - 6 ;∈ b = 520 × 10 - 6 e ∈ c = - 450 × 10 - 6 . Det
Considere o caso geral de deformação plana na qual ϵ x ,ϵ yeγ x y são conhecidas. Escreva um código computacional que possa ser usado para determinar a deformação normal e a deformação por cisalhament