Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 2.Problemas - Ex. 19

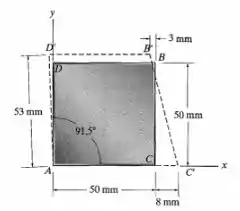
O quadrado deforma-se até chegar à posição mostrada pelas linhas tracejadas. Determine a deformação por cisalhamento em cada um de seus cantos A, B, C e D. O lado D’B’ permanece horizontal.

Passo 1

Falaa, a deformação por cisalhamento é a variação angular nos vértices da nossa figura. Então a gente precisa achar cada um desses ângulos finais e substrair de 90 °   ( π / 2 ) (ângulo inicial dos vértices).

Primeiro, vamos esquematizar a situação:

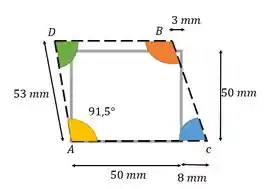
Bora olhar cada vértice. Vem!

Passo 2

O A é o mais tranquilo porque ele já dá o ângulo fina, né? A deformação fica

γ A = π 2 - π 180 × 91,5 ° = - 0,0262   r a d

Repara que a resposta final fica em radianos.

Passo 3

Daí a gente pode olhar o vértice D . Se a gente passar uma reta vertical pelo ponto A , temos algo assim:

Como a soma dos ângulos do triângulo é 180 ° e li temos um ângulo reto:

91,5 ° - 90 ° + 90 ° + θ D = 180 ° → θ D = 88,5 °

A deformação fica:

γ D = π 2 - π 180 ° × 88,5 ° = 0,0262   r a d

Passo 4

O ângulo em C podemos achar por trigonometria:

θ C ' = a r c t g 53 cos ⁡ 91,5 ° - 90 ° 8 + 3 = 78,27 °

γ C = π 2 - π 180 × 78,27 ° = 0,205   r a d

θ B ' = 360 ° - 88,5 ° - 91,5 ° - 78,27 ° = 101,73 °

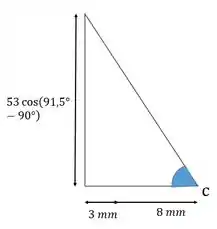
Passo 5

Como a soma de ângulos de um quadrilátero é 360   ° , achamos o ângulo de B :

θ B ' = 360 ° - 88,5 ° - 91,5 ° - 78,27 ° = 101,73 °

γ B = π 2 - π 180 ° × 101,73 ° = - 0,205   r a d

Resposta

γ A = - 0,0262   r a d

γ D = 0,0262   r a d

γ B = - 0,205   r a d

γ C = 0,205   r a d

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O estado plano de tensões mostrado ocorre em uma barra feita de uma classe de aço, com uma resistência ao escoamento na tração de 240M P a . Determinar o coeficiente de segurança, em relação ao escoam
O estado plano de tensões mostrado ocorre em um componente estrutural feito de aço com σ e = 250M P a . Usando o critério da máxima energia de distorção, determinar se o escoamento ocorre quando: (a)
O estado plano de tensões mostrado ocorre em uma barra feita de uma classe de aço, com resistência ao escoamento na tração de 300M P a . Determinar o coeficiente de segurança, em relação ao escoamento
Um eixo de 36m m de diâmetro é feito de uma classe de aço, com uma resistência ao escoamento na tração de 250M P a . Usando o critério da máxima energia de distorção, determinar a intensidade do torqu
O estado plano de tensões mostrado ocorre em uma barra feita de uma classe de aço, com resistência ao escoamento na tração de 300M P a . Determinar o coeficiente de segurança, em relação ao escoamento