Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 3.Problemas - Ex. 9
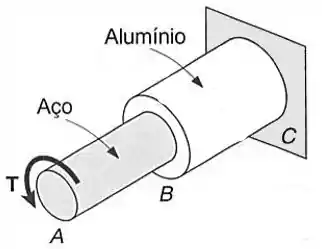
O eixo é feito de um aço com tensão admissível ao cisalhamento de , e o eixo é feito de uma liga de alumínio com tensão admissível de cisalhamento de . Sabendo-se que o diâmetro do eixo é de , e desprezando-se o efeito da concentração de tensões, determine: (a) o maior torque que pode ser aplicado em , se a tensão admissível não pode ser excedida ao eixo ; (b) o correspondente diâmetro necessário para o eixo .
Passo 1
Para resolver a letra A vamos ter que aplicar a equação da torção, que é a seguinte:
Onde:
- Representa a tensão de cisalhamento.
- A torção a qual a barra está submetida.
- A distância do centro ao ponto de aplicação.
- O momento de inércia polar.
Lembrando que o momento de inércia polar é calculado como:
Na letra A os dados foram os seguintes:
- Tensão de cisalhamento máxima admissível
- Diâmetro do eixo.
Isso é tudo para podermos calcular o maior torque que pode ser aplicado em A.
Passo 2
Para calcular esse torque vamos substituir na equação, calculando primeiro o momento de inércia polar.
Passo 3
Agora é só substituir na equação, lembrando que o maior torque acontece no ponto mais externo
Passo 4
Agora para responder a letra B vamos pegar a torção da letra A e descobrir o diâmetro de
Mas não temos nem logo vamos utilizar a equação de
E substituir na de cima
Resposta
a)
b)