Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 4.Problemas - Ex. 39
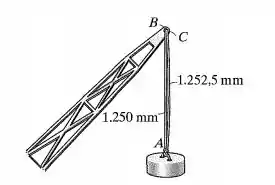
A carga de deve ser suportada pelos dois cabos verticais de aço para os quais . Se os comprimentos originais dos cabos e forem e respectivamente, determine a força desenvolvida em cada cabo depois da suspensão da carga. Cada cabo tem área de seção transversal de
Passo 1
Falaa!
Vamos entender a situação do nosso problema. Temos dois cabos de aço, um é maior que o outro. Eles dois juntos precisam suportar a carga juntos. Cada um vai resistir a uma parcela dessa carga. E é isso que ele quer saber, a força em cada cabo.
Bora fazer um DLC da carga no ponto dos cabos:
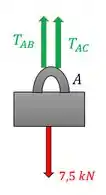
Com isso, podemos utilizar a fórmula do equilíbrio no eixo :
Percebe que a gente tem apenas uma equação que relaciona essas duas incógnitas que queremos achar? Precisamos então de mais uma equação.
Passo 2
Vamos tentar achar essa equação que falta da compatibilidade de deslocamentos.
No início da situação, sem carga, o cabo AB está retinho, mas o AC está frouxo porque ele é maior. Mas por causa da carga, eles vão ser esticados e alongados. Algo assim:
No processo de aplicação da carga, primeiro o cabo que já estava reto vai ser deformado enquando o outro cabo maior vai só ficar reto, nisso o ponto desce para Aí depois os dois cabos sofrem um alongamento, aí o ponto desce e vai para .
Aí da figura, vemos que o alongamento total do cabo AB é igual a mais o alongamento de . Aí podemos escrever assim:
Passo 3
Agora, temos que aplicar a fórmula de para cada um:
Fica assim:
Aqui é importante notar que a gente pode considerar que
Essa é nossa segunda equação.
Passo 4
Agora, achamos as pelo sisteminha de suas equações:
Isolando na equação de cima e substituindo na segunda:
Isolando
Substituindo isso na primeira equação, e isolando :