Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 7.Problemas - Ex. 161

O eixo maciço AB e as engrenagens mostradas são usadas para transmitir 15 hp do motor M para uma máquina conectada a um eixo maciço CDE. Sabendo –se que o motor gira a 360 rpm w que tadm= 50 MPa, determinar o menor diâmetro permissível para eixo AB.

Passo 1

Fala aíi gurizada tudo belezinha, espero que simm!!!! Antes de começarmos vamos desenhar um esboço para conseguirmos enchergar melhor as forças e os valores

Prontinhooo, são várias etapas até encontrarmos o diâmetro, mas vamos aos pouquinhos, passo a passo, primeiramente vamos achar a frequência, vejam...

f = 360 60 = 6   H Z

P =   15 × 6600 = 99000   c m / s

Agora podemos encontrar o torque em D.. a fórmula a ser usada é esta abaixo :D

T = P 2 π f

T = 99000 2 π × 6 = 2,62 ×   10 3   N m

Galera vamos considerar que o torque em E é igual ao D= 2,62 ×   10 3   N m

As forças das engrenagens D e E são calculadas abaixo:

F d = T r = 2,62 ×   10 3 96 ×   10 - 3 = 27,35 ×   10 3   N

F e = T r = 2,62 ×   10 3 60 ×   10 - 3 = 43,66 ×   10 3   N

Agora gurizadaaa vamos esboçar um diagrama das forças horizontais

∑ F h = 0

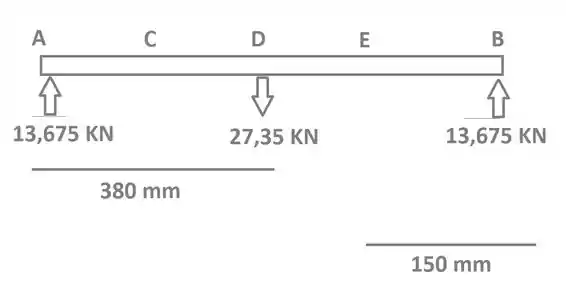
Vamos esboçar onde os momentos indicados pelas distancias atuam, pois se tratando de torção teremos que levar em consideração as forças na vertical também, que veremos em breve....

+ ↶ ∑ M = F × d

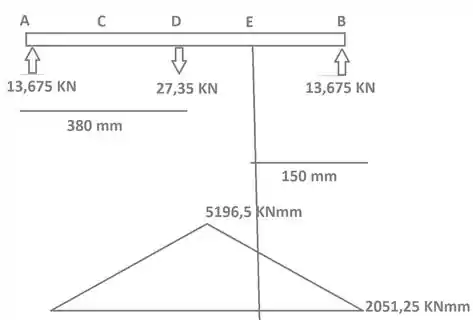
Passo 2

Agora vamos esboçar para as forças verticais, na mesma analogia ...

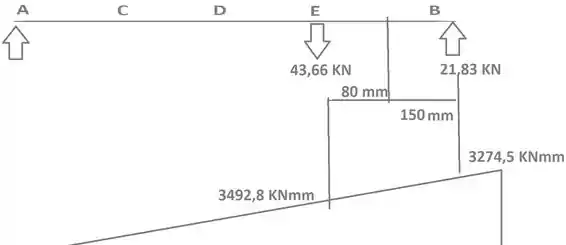
Agora podemos encontrar os momentos em E e D

+ ↶ ∑ M = F × d

M d = 3492,8 2 + 5196,5 ² = 6261,25   K N m m

M e = 3 274,5 2 + 2051,25 ² = 3863,63   K N m m

Agora teremos que usar a tensão admissível dada no exercício para enfim encontrarmos o diâmetro ...neste caso encontraremos o raio antes...

τ = π 2 r ³   × M 2 + T ²

50 × 10 6 = π 2 r ³   × ( 6261,25 ×   10 3 ) ² + ( 2,62 ×   10 3 ) ²

r =   0,43   m m

d = 2 r = 0,86   m m

Resposta

d = 0,86   m m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma barra de 18m m de diâmetro deve ser encurvada devido às cargas aplicadas, como mostrado. Sabendo-se que P = 200N e Q = 0 , determinar a máxima tensão de cisalhamento e a máxima tensão normal, na e
Derivar a Eq. (733), a qual define a tensão vertical σ y , em uma viga retangular de largura unitária e altura 2 c , sujeita a uma carga distribuída w ( x ) .
Uma barra de 18m m de diâmetro deve ser encurvada devido às cargas aplicadas, como mostrado. Sabendo-se que P = 200N e Q = 0 , determinar a máxima tensão de cisalhamento e a máxima tensão normal, na e
Usando a expressão dada no Prob7.172 , determinar ( a ) a seção transversal do eixo do Prob. Resolvido 7.12 , para que a máxima tensão normal ocorra; ( b ) o valor da σ m á x á , sabendo-se que o diâm
Para as barras e carregamento do prob 169 e usando a expressão dada no problema 7.172, determinar a máxima tensão normal na: ( a ) Barra B C ; ( b ) na barra C D