Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 3.Problemas - Ex. 12

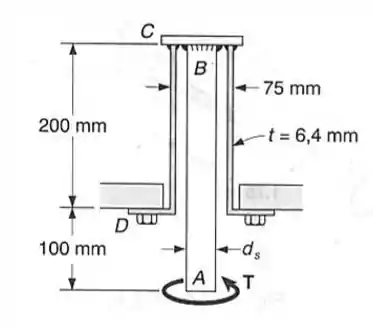
O eixo maciço A B é feito de um aço, com uma tensão admissível ao cisalhamento de 80   M P a e o tubo C D é feito de latão, com uma tensão admissível ao cisalhamento de 50   M P a . Determinar: (a) o maior torque T que pode ser aplicado em A , se a tensão admissível não pode exceder a do tubo C D ; (b) o correspondente valor do diâmetro d s necessário ao eixo A B .

Passo 1

Neste exercício temos dois tubos sujeitos à mesma torção, porém devido à geometria de cada um deles a tensão de cisalhamento será diferente. Por isso, vamos ter que calculara tensão para o tubo C D e, posteriormente, calcular o diâmetro d s utilizando a equação da torção:

τ = T ⋅ c J

Onde:

  • τ Representa a tensão de cisalhamento.
  • T A torção a qual a barra está submetida.
  • c A distância do centro ao ponto de aplicação.
  • J O momento de inércia polar.

Lembrando que o momento de inércia polar é calculado como:

J = π ⋅ c 4 2

Passo 2

Vamos calcular a torção máxima admissível em C D . Primeiro calculando o momento de inércia polar.

J = π ⋅ c 4 2

Como é uma barra vazada

J = π ⋅ c e x t 4 2 - π ⋅ c i n t 4 2

J = π ⋅ ( c e x t 4 - c i n t 4 ) 2

J = π ⋅ [ 75 × 10 - 3 4 - ( 75 - 6,4 ) × 10 - 3 4 ] 2

J = π ⋅ [ 75 × 10 - 3 4 - 68,6 × 10 - 3 4 ] 2

J = π ⋅ [ 31640625 × 10 - 12 - 22146059 × 10 - 12 ] 2

J = π ⋅ ( 31640625 - 22146059 ) × 10 - 12 2

J = π ⋅ 9494565,5 × 10 - 12 2

J = 14914028 × 10 - 12 m 4

Passo 3

Aplicando na equação do torque:

τ = T ⋅ c J

Como c é a maior distância do centro à superfície:

c = 75 - 6,4   m m

c = 68,6 × 10 - 3   m

5 0 × 10 6 = T ⋅ 68,6 × 10 - 3 14914028 × 10 - 12

50 × 10 6 ⋅ ( 14914028 × 10 - 12 ) = T ⋅ 68,6 × 10 - 3

T ⋅ 68,6 × 10 - 3 = 50 × 10 6 ⋅ ( 14914028 × 10 - 12 )

T = 50 × 10 6 ⋅ 14914028 × 10 - 12 68,6 × 10 - 3

T = 50 ⋅ 14914028 68,6 ⋅ 10 6 ⋅ 10 - 12 10 - 3

T = 10870282,8 ⋅ 10 - 3   N . m

T = 10870 , 3   N ⋅ m

Passo 4

A partir do torque calculado vamos calcular o diâmetro d s :

τ = T ⋅ c J

Como o momento de inércia polar é dado como:

J = π ⋅ c 4 2

vamos ter:

τ = T ⋅ c π ⋅ c 4 2

τ = 2 ⋅ T ⋅ c π ⋅ c 4

τ = 2 ⋅ T π ⋅ c 3

Agora basta substituir os valores:

80 × 10 6 = 2 ⋅ 10870,3 π ⋅ c 3

c 3 = 2 ⋅ 10870,3 π ⋅ 80 × 10 6

c 3 = 86,50 × 10 - 6

c = 86,50 × 10 - 6 3

c = 86,50 3 ⋅ 10 - 6 3

c = 4,42 ⋅ 10 - 2   m

c = 4 4 , 2 ⋅ 10 - 3   m

c = 44,2   m m

d s = 2 ⋅ c

d s = 2 ⋅ 44,2

d s = 88,4   m m

Resposta

a)

T = 10870,3   N ⋅ m

b)

d s = 88,4   m m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O eixo tem diâmetro de 80mm e, devido ao atrito na superfície no interior do furo, está sujeito a um torque variável descrito pela função t = 25 x ⋅ e x 2Nm/m , onde x é dado em metros. Determine o to
O elo funciona como parte do controle do elevador de um pequeno avião. Se o tubo de alumínio conectado tiver 25mm de diâmetro interno e parede de 5mm de espessura, determine a tensão de cisalhamento m
O eixo maciço tem conicidade linear de r A em uma extremidade e r B na outra extremidade. Deduza uma equação que dê a tensão de cisalhamento máxima no eixo em uma localização x ao longo da linha centr
O eixo é composto por três tubos concêntricos, todos do mesmo material, e cada um com os raios internos e externos mostrados na figura. Se for aplicado um torque T = 800Nm ao disco rígido preso à sua
O tubo de cobre tem diâmetro externo de 62,5mm e diâmetro interno de 57,5mm . Se estiver firmemente preso à parede em C e for submetido a um torque uniformemente distribuído ao longo de todo o seu com