Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 5.Problemas - Ex. 87
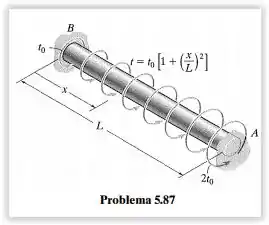
O eixo de raio é submetido a um torque distribuído , medido como torque/comprimento do eixo. Determine as reações nos apoios A e B.
Passo 1
Olá pessoal, vamos ao trabalho!!
A questão quer que determinemos a torção em () e a torção em (, para isso iremos realizar um somatório de torques depois igualar os ângulos de deformação causados pelos torques diferente, sendo que como os pontos e são fixos não haverá rotação. Temos que:
Passo 2
No momento vamos analisar a figura para uma melhor visualização do próximo passo.
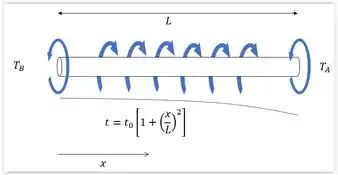
Primeiramente vamos encontrar qual é a equação que rege o torque resultante () do carregamento .
Sendo assim, o torque do carregamento máximo ocorre quando o que será;
Se fosse realizar agora o somatório dos torques teríamos uma equação para duas incógnitas, para isso vamos primeiro relacionar as deformações provocadas pelos torques.
Fixando somente o ponto temos que no ponto haverá dois ângulos de deformação por torção gerados: um por () e outro por (). Porém como sabemos que é fixado, logo sua . Então, temos:
Passo 3
Agora só realizar o somatório e encontrar o valor de .