Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 3.Problemas - Ex. 88
O eixo seção variável mostrado na figura deve transmitir kW. Sabendo que a tensão de cisalhamento admissível no eixo é de MPa e que o raio do adoçamento é, determine a rotação possível no eixo.
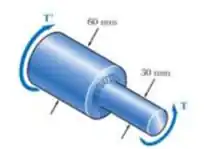
Passo 1
E ai gurizada tudo belezinha? O enunciado pede que a gente determine a rotação possível no eixo. Comecemos trazendo alguns dados.
Sabendo que e podemos determinar o torque a partir da tensão de cisalhamento
Agora precisamos determinar a frequência sabendo que
Resposta
Então galerinha, depois desse cálculo, descobrimos que a rotação é .
Exercícios de Livros Relacionados
A curva mostrada na F i g .P 3.89 e F i g .P 3 . 92 pode ser aproximada pela relação: τ = 27,8x10 9γ - 1,390x10 12γ 2 Usando esta relação e as equações (3.2) e (3.26) resolver o problema indicado.
Um eixo vazado de diâmetro interno e externo iguais a 20 m me50 m m , respectivamente, é fabricado de uma liga de alumínio, cujo diagrama τ - γ é mostrado. Determinar:O torque necessário para torcer u
O eixo maciço mostrado é feito de um aço doce, que é considerado ser elastoplástico com G = 77G P a e τ e = 145M P a . Sabendo-se que um torque T de 980N m é aplicado ao eixo e depois removido, determ
No Prob. 3.97, determinar o ângulo de torção permanente no eixo.
No Prob. 3.96, determinar o ângulo de torção permanente no eixo.