Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 3.Problemas - Ex. 106

Um eixo de seção vazada tem 0,9 m de comprimento e a seção transversal mostrada. O aço é considerado elastoplástico com τ E = 180   M P a e G = 77,2     G P a . Determine a o ângulo de torção quando a seção se torna inteira plástica e b a correspondente intensidade do torque aplicado.

Passo 1

E ai gurizada tudo belezinha? Espero que sim!! O enunciado pede que a gente determine o ângulo de torção quando a seção se torna inteira plástica e a correspondente intensidade do torque aplicado.

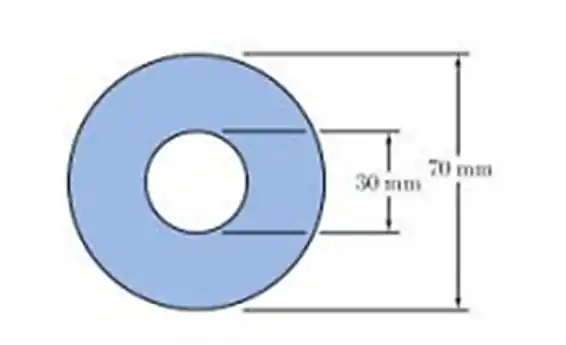
Então vamos, notem abaixo as medias do nosso eixo, e partiu calcular !!!

c 1 = 1 2 d 1 = 0,015   m c 2 = 1 2 d 2 = 0,035   m

Para determinarmos o ângulo de torção quando a seção se torna inteira plástica, consideramos que:

ρ Y = c 1

t = t E   = y = τ E G = p y φ L = c 1 φ L

Isolando o ângulo temos:

φ = L t y c 1 G = 0,9 180 x 10 6 0,015 77,2 x 10 6 = 139,90 x 10 - 3   r a d

φ = 8,02 °

Passo 2

Na questão B ele pede para que a gente encontre o torque correspondente a intensidade do torque aplicado, e partiremos da integral a seguir.

T P = 2 π ∫ c 1 c 2 τ E   p 2   d p = 2 π τ y p 3 3 ∫ c 1 c 2 2 π 3 τ E c 2 3 - c 1 3

= 2 π 3 180 x 10 6 0,035 3 - 0,015 3 = 14,89 x 10 3 N ⋅ m = 14,89   k N ⋅

Resposta

  1. φ = 8,02 °
  2. 14,89   k N ⋅ m .
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O eixo composto mostrado consiste em uma jaqueta de latão de 5.08 mm de espessura ( G l a t ã o = 39G P a ) ã unido a um núcleo de aço de 40 mm de diâmetro G a ç o = 77.2G P a ç . As tensões de cisalh
Dois eixos de aço sólidos são ajustados com flanges que em seguida são conectadas por parafusos como mostrado. Os parafusos são ligeiramente subdimensionados de modo que permitam uma rotação relativa
Os cilindros de seção transversal cheia AB e BC estão conectados em B e engastados em suportes fixos de A e em C. Sabendo os módulos de rigidez são 77,2 GPa para o alumínio e 38.6 GPa para o latão, de
Para o eixo de seção circular do Problema 3.94, determine o ângulo de giro causado pela aplicação de um torque de intensidade (a) T = 80k i p ⋅ i n e (b) T = 130k i p ⋅ i n .
Dois eixos de aço sólidos são ajustados com flanges que em seguida são conectadas por parafusos como mostrado. Os parafusos são ligeiramente subdimencionados de modo que permitam uma rotação relativa