Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 3.Problemas - Ex. 57

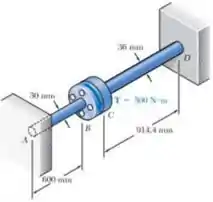
Dois eixos de aço sólidos são ajustados com flanges que em seguida são conectadas por parafusos como mostrado. Os parafusos são ligeiramente subdimencionados de modo que permitam uma rotação relativa entre os flanges de até 1.5° antes que ambas comecem a girar juntas. Sabendo que G = 77.2 GPa, determine a máxima tensão de cisalhamento em cada eixo quando um torque T de intensidade igual 500 N/m é aplicada na flange indicado. O torque T é aplicado no flange B.

Passo 1

E ai gurizada tudo belezinha? Não se assustem com o tamanho do enunciado porque aos poucos passo a passo vamos conseguir resolve-lo :D . Primeiramente vamos considerar o eixo:

Eixo AB:

T = T A B , L = 0,6   m c = 1 2 d = 0,50 × 0,030 =   0,015   m

Achando J temos:

J A B = π 2 c 4 = π 2 0,015 4 = 79,522 × 10 - 9 m 4

E o ângulo é dado por:

φ B = T A B L A B G A B J A B T A B = G A B J A B L φ B   = 77,2 × 10 9 79,522 × 10 - 9 0,6 φ B = 10,2318 × 10 3 φ B

Passo 2

Agora vamos fazer o eixo CD:

T = T C D L C D = 0,914   m c = 1 2 d = 0,018   m

Achando J temos:

J C D = π 2 c 4 = π 2 0,018 4 = 164,896 × 10 - 9   m 4

E o ângulo é dado por:

T C D = G C D J C D L C D

φ C = 77,2 × 10 9 164,896 × 10 - 9 0,914 = 13,9277 × 10 3 φ C

Verificamos a rotação de folga da flange B:

φ B ' = 1,5 ° = 26,178 × 10 - 3 r a d

Vamos ao valor do torque que diminui a folga:

T A B ' = 10,2318 × 10 3 26,178 × 10 - 3 = 267,85   N / m

O torque T " para causar rotação adicional em φ " :

T " = 500 - 267,85 = 232,15   N / m

T " = T " A B + T " C D 232,15 = 10,2318 × 10 3 + 13,9277 × 10 3 φ "

φ " = 10,4068 × 10 - 3 r a d

Agora que achamos o ângulo podemos determinar o torque nas seções:

T " A B = 10,2318 × 10 3 10,4068 × 10 - 3 = 106,480   N / m  

T " C D = 13,9277 × 10 3 10,4068 × 10 - 3 = 144,942   N / m

Passo 3

Agora, vamos fazer a tensão de cisalhamento em AB:

τ A B = T A B c J A B = 267,85 + 106,4802 0,015 79,522 = 70,61   × 10 6 P a

τ A B = 70,61   M P a

Vamos para tensão máxima de cisalhamento em CD:

τ C D = T C D c J C D = 144,942 0,018 164,896 = 15,83 × 10 6 P a

τ C D = 15,83   M P a

Resposta

τ A B = 70,61   M P a e τ C D = 15,83   M P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Sabendo-se que a varra do Prop 3.127 tem 900 mm de comprimento e que G = 26G P a , determinar o ângulo de torção causado pelo torque 1,2 kNm
Um eixo cilíndrico vazado foi projetado com a seção transversal mostrada na Fig (1) para resistir a um torque máximo T 0 . Um defeito na fabricação, no entanto, resultou em uma pequena excentricidade
As especificações de projeto de um eixo de transmissão de seção cheia de 1,2 m de comprimento requerem que o ângulo de torção do eixo não exceda 4° quando for aplicado um torque de 750N / m . Determin
A haste cilíndrica cheia BC de comprimento L = 24i n . é conectada na alavanca rígida AB de comprimento a = 15i n , e no suporte C. Especificações de projeto exigem que o deslocamento de A não exceda
A haste cilíndrica cheia BC de comprimento L = 24i n . é conectada na alavanca rígida AB de comprimento a = 15i n , e no suporte C. Especificações de projeto exigem que o deslocamento de A não exceda