Para uma viga extrudada, com a seção transversal mostrada, determinar:
- A localização do centro de cisalhamento O.
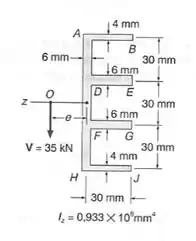
Passo 1
Para esse tipo de questão sabemos que a nossa tensão de cisalhamento produz na seção forças que são decorrentes do diagrama de tensões. Mas ai temos o seguinte macete, imagine que na verdade a nossa seção tenha o seguinte fluxo de tensões.
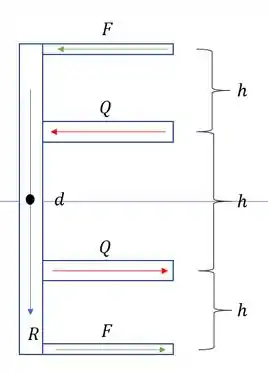
Se calcularmos o momento fletor em torno de “d” teremos que:
Agora pensa o seguinte, se temos esse momento fletor agindo em torno de “d” vamos tentar equilibrar ele, e para equilibrar, precisamos descobrir qual a distância “e” que podemos colocar a nossa carga vertical para garantir que a nossa seção vá descer vertical, e não rotacionar, sendo assim, teremos que:
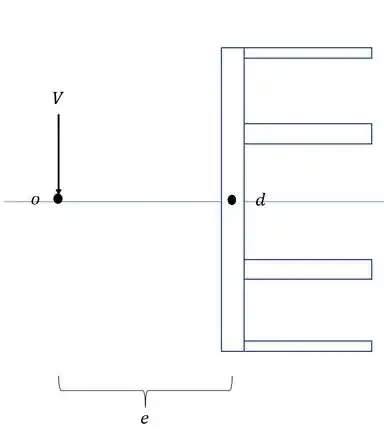
Calculando o momento fletor em “d” teremos que:
E igualando os momentos fletores, teremos que:
Sabemos que a força que age na seção superior e gera a força é dada pela seguinte equação:
Sabemos que:
Agora vamos determinar cada um dos nossos termos, bora nessa?
Passo 2
O momento de inércia da nossa seção já foi dado no enunciado, e com isso temos que:
A espessura de cisalhamento vai depender do local que estamos calculando a tensão, sendo assim teremos que:
- Força F
- Força Q
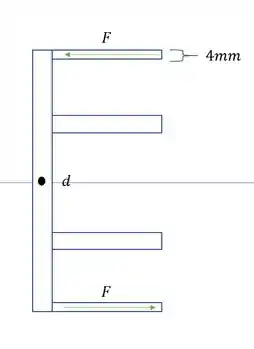
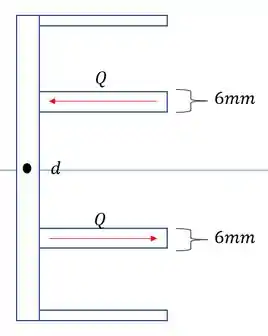
Vamos agora para a definição do momento estático.
Passo 3
Para o momento estático, precisamos escrever a nossa equação em função disso, porque sabemos que a nossa força está em função da tensão, mas para isso temos que calcular cada uma das forças separadamente, vamos então fazer o seguinte, bora começar pela força F, e depois calculamos a força Q, vamos nessa?
- Força em F
- Área da região acima do ponto que se quer saber o cisalhamento
- Distância do centroide da área até a LN
- Tensão
- Força em Q
- Área da região acima do ponto que se quer saber o cisalhamento
- Distância do centroide da área até a LN
- Tensão
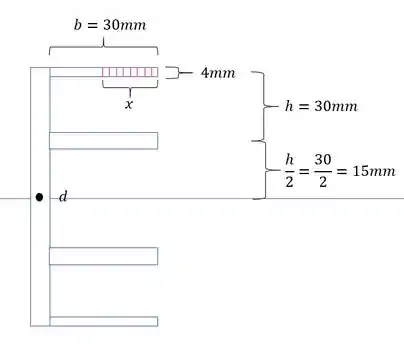
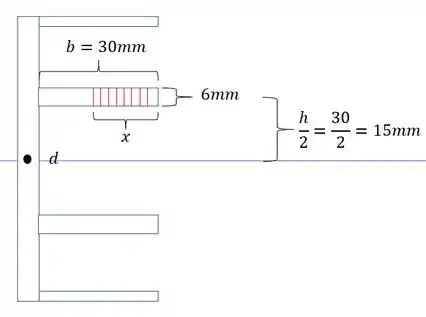
Lembrando que x é a variação do comprimento da área analisada.
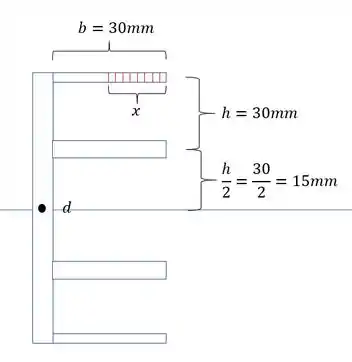
agora para determinar o momento estático precisamos fazer a seguinte conta:
E sabemos que a espessura de cisalhamento é dado por . substituindo isso na nossa equação teremos que:
Sabemos que devemos substituir isso na seguinte integral:
Sabemos que:
Logo:
Sendo assim teremos que:
Como sabemos que x varia de 0 até 30, podemos ignorar o zero e analisar apenas o 30, sendo assim teremos que:
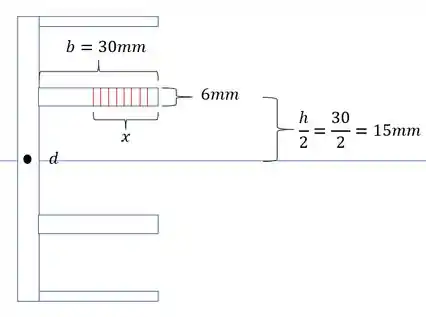
Lembrando que x é a variação do comprimento da área analisada.
agora para determinar o momento estático precisamos fazer a seguinte conta:
E sabemos que a espessura de cisalhamento é dado por . substituindo isso na nossa equação teremos que:
Sabemos que devemos substituir isso na seguinte integral:
Sabemos que:
Logo:
Sendo assim teremos que:
Como sabemos que x varia de 0 até 30, podemos ignorar o zero e analisar apenas o 30, sendo assim teremos que:
Mas lembra o nosso objetivo? Queremos determinar a excentricidade que podemos aplicar a nossa carga, sendo assim, como já temos a força, teremos que: