Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 3.Problemas - Ex. 21

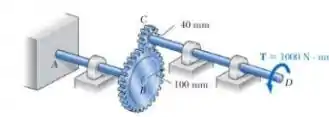
Um torque de intensidade T = 1000 N/m é aplicado em D. como mostra a figura. Sabendo que a tensão de cisalhamento admissível é a de 60 MPa em cada eixo, determine o diâmetro necessário do (a) eixo AB e (b) eixo CD .

Passo 1

Galerinha, vamos começar pegando alguns dados.

T C D = 1000   N / m

T A B = r b r c       T c d = 100 40 1000 = 2500   N / m

vamos começar com o eixo AB.

τ a l l = 60 × 10 6   P a

τ = T c J = 2 T π τ         c 3 = 2 T π τ = 2 2500 π 60 × 10 6 = 26.526 × 10 - 6   m 3

c = 29,82 × 10 - 3 = 29,82   m m d = 2 c = 59,6   m m

Passo 2

Então agora seguimos para o eixo CD, sabendo que > τ all =60× 10 6   Pa

τ = TC J = 2T π c 3   c 3 = 2 T π τ = 2 1000 π 60 × 10 6 = 10.610 × 10 - 6   m 3

c=21,97× 10 -3  m = 21,97 mm      d=2c=43,9 mm

Resposta

  1. AB = 59,6 mm
  2. CD 43,9 mm.
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determinar:O torque T que causará uma tensão de cisalhamento máxima de 45M p a no cilindro vazado de aço, como indicado;A máxima tensão de cisalhamento causada pelo mesmo torque T, em um eixo cilíndri
Determine:O torque que pode ser aplicado a um eixo maciço de 75m m de diâmetro sem que seja excedida a tensão admissível de cisalhamento de 83M p a ;Idem ao item a), considerando que o eixo maciço dev
Os torques são exercidos nas polias A, B e C. Sabendo-se que ambos os eixos são maciços, determinar a máxima tensão de cisalhamento:No eixo AB;No eixo BC.
Sob condições normais de operação, um motor elétrico exerce um torque de 1350N m , em E . Sabendo-se que todo o eixo é maciço, determinar a máxima tensão de cisalhamento:No eixo BC;No eixo CD;No eixo
Resolver o P r o b .3.6 , considerando que um furo de diâmetro igual a 25,4 m m foi broqueado ao longo de todo o eixo.