Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 5.Problemas - Ex. 123
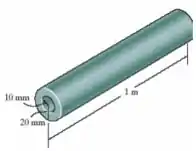
Um eixo tubular tem diâmetro interno de , diâmetro externo de e comprimento de . É feito de um material elástico perfeitamente plástico, com tensão de escoamento . Determine o torque com tensão de escoamento . Determine o torque máximo que ele pode transmitir. Qual é o ângulo de torção de uma extremidade em relação à outra extremidade se a deformação por cisalhamento na superfície interna do tubo estiver prestes a escoar?
Passo 1
Dados da questão:
Para resolver a questão temos que primeiro calcular o torque plástico que atua no eixo utilizando a equação 5.23.
E para determinar o ângulo de torção usaremos a Equação 5.25
Passo 2
Vamos determinar o torque usando a equação 5.23, onde os limites de integração são os diâmetros interno e externo.
Como não há núcleo elástico, a tensão é constante e igual à tensão de escoamento:
Efetuando a integração
Aplicando os valores
Como essa é uma sessão vazada não podemos aplicar a equação 5.26 pois ela só é válida para eixos maciços.
Passo 3
Vamos determinar o momento de inércia da seção:
Passo 4
A questão também afirma que o material é elástico perfeitamente plástico. Isso quer dizer que a tensão do material se comporta como o gráfico abaixo.
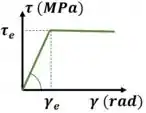
O nosso ponto de interesse é o raio interno! Como a quetão afirma que ele está “preste a escoar” podemos afirmar que sua tensão é igual a tensão de escoamento e sua deformação é igual a deformação de escoamento.
No exato ponto do escoamento, a lei de hooke ainda é válida. Dessa forma, podemos determinar a deformação que atua na parte interna do eixo
Passo 5
Aplicamos agora a equação 5.25 no nosso ponto de interesse, que é o raio interno