Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 5.Problemas - Ex. 129
O eixo é composto por duas seções rigidamente acopladas. Se o material for elástico perfeitamente plástico como mostra a figura, determine o maior torque T que pode ser aplicado eixo. Além disso, desenhe a distribuição da tensão de cisalhamento na linha radial para cada seção. Despreze o efeito da concentração de tensão.
Passo 1
Dados da questão:
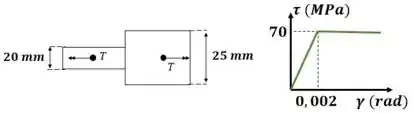
A questão pede:
- O maior torque que atua sobre o eixo
- Esboço da distribuição de tensão
A gente pode pensar assim: para acharmos o maior torque que pode ser aplicado, vamos analisar o eixo mais fino. Por que? Porque o eixo menos fino consegue resistir a um torque maior, um torque que o mais fino não resistiria, ok?
Bora lá!
Passo 2
Como nosso material é perfeitamente elástico-plástico, o torque máximo dele não ocorre na tensão máxima, a de escoamento.
Podemos continuar aumentando o torque, mesmo depois de atingir essa tensão. Aí nosso elemento entra no regime plástico. E para calcular a tensão plástica máxima sobre um eixo, podemos usar:
Substituíndo os valores:
Passo 3
A tensão sobre o diâmetro menor já é conhecida (é a máxima). Mas precisaremos calcular a tensão sobre o diâmetro maior. Essas tensões vão ser diferentes porque eles tem áreas diferentes.
Para isso precisaremos do momento de inércia
Passo 4
Vamos ver se a tensão sobre o diâmetro maior é elástica, usando a fórmula do torque elástico. Aí vai ser o torque máximo que a gente achou.
Passo 5
Podemos agora contruir nosso esboço.
Como o eixo mais fino está no limite do regime elástico, a distribuição de tensão nele vai ser totalmente constante ao longo do raio.
Já como o eixo maior está no regime totalmente elástico, a distribuição de tensão nele vai ser linear e crescente com o raio.
Aí ficamos assim:
Obs: o gabarito do livro está com um errinho nessa, tá?