Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 13.Problemas - Ex. 126
O elemento estrutural feito de liga de alumínio 2014-T6 tem seção transversal simétrica. Se estiver acoplado por pinos nas extremidades, determine a maior força que ele pose suportar.
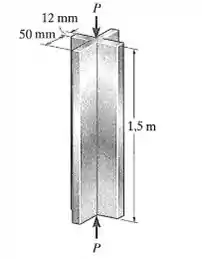
Passo 1
Como está preso por pinos nas extremidades,
Primeiramente, calculando-se a área e o momento de inércia, teremos:
Calculando-se o , teremos:
Passo 2
Agora, vamos calcular o índice de esbeltez:
Como é maior que 55, podemos usar a fórmula:
Vimos que é menor que a tensão de escoamento, logo:
Resposta
Exercícios de Livros Relacionados
21. A coluna de 3,0m tem as dimensões mostradas na figura. Determine a carga crítica, se a base for engastada e o topo estiver preso por pinos. E m = 12G P a , σ e = 35M P a .
23. Resolva o Problema 13.22 no caso de um elemento estrutural A B com raio de 50m m
22. Consideramos que os elementos estruturais da treliça estão acoplados por pinos. Se o elemento estrutural BD for uma haste de aço A - 36 de raio 50m m , determine a carga máxima P que pode ser supo
Considere uma coluna ideal com uma extremidade engastada e uma presa por pino. Mostre que a carga crítica é dada por P c r = 20,19 E I L 2 . .
A coluna ideal está sujeita à força F em seu ponto médio e à carga axial P. Determine o momento máximo da coluna no meio do vão.