Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 6.Problemas - Ex. 170
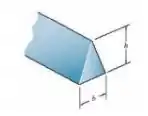
O elemento é feito de material elástico perfeitamente plástico para o qual σe = 230 MPa. Determine o momento elástico máximo e o momento plástico que podem ser aplicados à seção transversal. Considere b = 50 mm e h = 80 mm.
Passo 1
Oi oi, meu xuxuzinho!! Tudo bem com você?? Vamos analisar o que a nossa questão nos pede e matar essa em 10 minutos?? Bora. Bom, nosso enunciado nos diz que essa viga tem um formato estranho, e nos pede os momentos plástico e elástico. Nem parece tão difícil, né?? Então bora fazer?? Partiu??
Passo 2
Nosso primeiro passo será calcular nossa posição da linha neutra, as forças de contração e tração, o momento de inércia e os momentos aplicados.
Passo 3
Agora que já temos todo o necessário para calcular nossos momentos, por que vamos esperar?? Só bora comigo.