Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 2.Problemas - Ex. 68

um tecido utilizado em estruturas infláveis está submetido a um carregamento biaxial que resulta em tensões normais σ x = 120   M P a   e   σ y = 160   M P a . Sabendo que as propriedades do tecido podem ser de aproximadamente E = 87   G P a   e   v = 0,34 , determine a variação no comprimento (a) do lado AB, (b) do lado BC e (c) da diagonal AC.

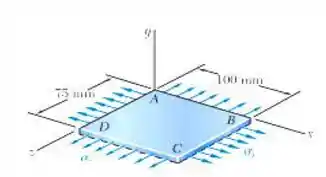
Passo 1

E ai gurizada tudo belezinha? Para determinarmos a variação no comprimento, antes vamos desenhar um esboço do diagrama de corpo livre para entendermos melhor como resolver esta questão, então vem comigo :D

Para determinarmos a variação do comprimento, vamos trazer os valores do enunciado

σ x = 120   M P a               σ y = 0               σ z = 160   M P a

Agora vamos ter que determinar a deformação em x e z aplicando a equação a seguir >D ε x = 1 E σ x - v σ y - v σ z = 1 87   x   10 9 120 x   10 6 - 0,34 -   16 0 x   10 6 = 459,77     x   10 - 6 ε z = 1 E - v σ x - v σ y + σ z = 1 87   x   10 9 - 0,34 -   120 x   10 6 + 160 x   10 6 = 459,77   x   10 - 6

Agora sim podemos determinar a variação de comprimento nas seções AB e BC, vem comigo gurizada :D

  1. δ A B = A B ε x = 100   x   459,77   x   10 - 6 = 45,97 . x   10 - 3   m m
  2. δ B C = B C ε Z = 75   x   459,77   x   10 - 6 = 34,48   x   10 - 3   m m

    3. Agora para encontrarmos na seção AC temos que utilizar Pitágoras vejam :D

    c ² = a ² + b ²

    .       c = 100 2 + 75 2  

      c = 125   m m

    Agora sim podemos determinar a variação de comprimento :D

  3. δ A C = 100 125   x   459,77   x   10 - 6 + 75 12 5   x   459,77   x   10 - 6 = 6,43 x   10 - 4 m m

Resposta

  1. 45,97 . x   10 - 3   m m
  2. 34,48   x   10 - 3   m m
  3. 6,43 x   10 - 4 m m
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Em muitas situações, sabe-se que a tensão normal em determinada direção é zero, como, σ z = 0 , no caso da placa fina mostrada. Para esse caso, conhecido como estado plano de tensão, mostre que, se as
O bloco plástico mostrado na figura é colado a um suporte rígido e a uma placa vertical à qual é aplicada uma força P de 55kip. Sabendo que, para o plástico utilizado, G = 150k s i determine o desloca
Dois blocos de borracha com um módulo de elasticidade transversal G = 10M P a são colados a dois suportes rígidos e a uma placa A B . Sabendo que b = 200m mec = 125m m , determine a maior força P admi
Um apoio de elastômero ( G = 130p s i ) é utilizado para suportar uma viga mestra de uma ponte, como mostra a figura, para proporcionar flexibilidade durante terremotos. A viga não pode sofrer desloca
Um quadrado de 1in, foi riscado na lateral de um grande vaso de pressão. Depois de pressurizado é mostrada a condição de tensão biaxial no quadrado. Sabendo que E = 29x10 6p s i e v = 0,30 , determine