Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 1.9 - Ex. 10
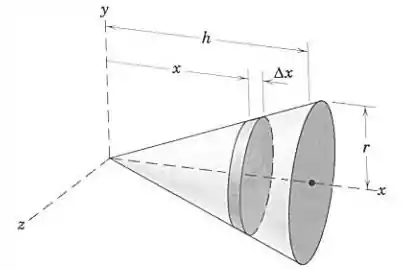
O elemento de volume do cone circular de altura e base de raio é formado cortando-se um elemento fino do cone a uma distância do vértice. Se o elemento cortado tiver uma espessura finita , mostre que seu volume vale . (Lembre-se da equação do volume de um cone.) Explique o que acontece ao segundo e terceiro termos quando se torna o infinitesimal .
Passo 1
Por razão de semelhança nos dois cones da figura, temos:
Lembre-se de que o volume de um cone é dado por:
Então, conforme o desenho, o volume de um cone de altura e raio da base é calculado assim:
Passo 2
Para calcular , devemos subtrair os volumes dos cones de altura e :
Passo 3
Quando tomamos o limite , os termos de ordem mais alta se anulam, de modo que:
Resposta
O segundo e terceiro termos se anulam:
Exercícios de Livros Relacionados
Para o suporte tipo gancho do Problema 2.1, usando trigonometria e sabendo que a intensidade de P é 75N , determine (a) a intensidade requerida da força Q se a resultante R das duas forças aplicadas e
Dois elementos estruturais A e B são parafusados a um suporte, como mostra a figura. Sabendo que ambos os elementos estão em compressão e que a força é 1 0k N no elemento A e 1 5k N no elementro B . D
Duas forças P e Q são aplicadas no ponto A de um suporte tipo gancho. Sabendo que P = 266N e Q = 110N , determine graficamente a intensidade, a direção e o sentido da resultante usando (b) a regra do
Para o suporte tipo gancho do Problema 2.7, determine usando trigonometria, (a) a intensidade e a direção da menor força P para que a resultante R das duas forças aplicadas no suporte seja horizontal,
Um tanque de aço deve ser posicionado em uma escavação. Sabendo-se que a intensidade de P = 2220N , determine, usando a trigonometria, (a) o ângulo requerido se a resultante R das duas forças aplicada