Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 7.3 - Ex. 24
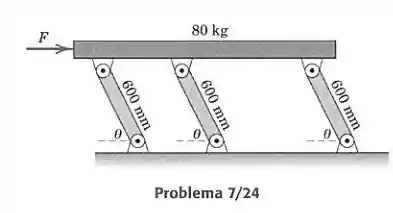
Especifique a força horizontal necessária para manter o equilíbrio da plataforma de 80 kg em função do ângulo feito pelas barras de sustentação em relação à horizontal. Cada uma das três barras uniformes tem uma massa de 10 kg. (Compare a solução por trabalho virtual com a solução pelo equilíbrio de forças e momentos.)
Passo 1
Utilizando o Princípio do Trabalho Virtual, se o sistema está em equilíbrio o trabalho virtual total realizado pelas forças externas ativas para um deslocamento pequeno do sistema deve ser zero:
Os nossos agentes externos ativos (que realizam trabalho em um deslocamento do sistema) são o peso de da plataforma, os pesos de de cada barra e a força As forças nos apoios não realizam trabalho, pois eles são fixos. Vamos calcular então o trabalho realizado por essas forças para um pequeno giro das barras, e então aplicar o princípio para encontrar em função de .
Passo 2
Primeiro vamos calcular o trabalho feito pelo peso da plataforma.
Agora o trabalho feito pelo pedo das três barras:
E, por último, o trabalho feito pela força :
Passo 3
Pelo Princípio do Trabalho Virtual, temos então:
Passo 4
Caso utilizássemos a solução pelo equilíbrio de forças e de momentos, teríamos que desmembrar nosso sistema, isolando em diagrama de corpo livre as barras e a placa de 80 kg. Apareceriam na nossa conta forças feitas entre a placa e as barras e nos apoios das barras com o chão. O método do trabalho virtual é muito mais vantajoso nesse caso.