Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 7.Problemas - Ex. 109
Quatro vigas de suportam uma carga de e são apoiadas, como mostrado, em uma longarina e em paredes de concreto. Sabendo-se que e , selecionar o perfil de abas largas que poderá ser usado: (a) para as vigas; (b) para a longarina .
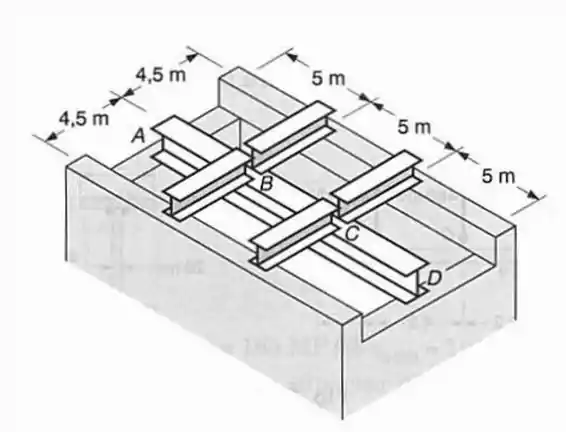
Passo 1
Oi, fala aí, galerinha!!! Para resolver esse problema a gente vai seguir o seguinte passo a passo:
- Calcular as reações nas vigas por meio das equações da estática.
- Calcular a força cortante, o momento fletor e achar o momento fletor máximo.
- Calcular o módulo resistente da seção .
- O item anterior nos fornecerá com um mínimo para que a viga resista às cargas. Selecionar aqueles em que e seja o mais econômico.
Então partiu pro exercício!
Passo 2
Para facilitar fazer um desenho das forças primeira para as vigas:
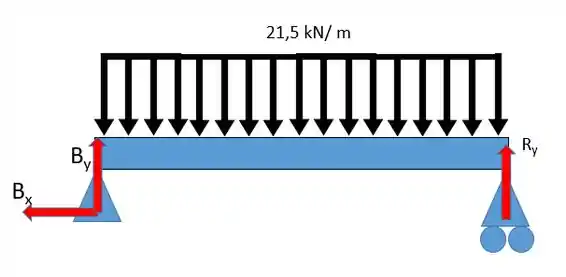
Agora vamos calcular as reações. Primeiro vamos perceber que não existem forças horizontais além de , logo, esta é nula. Com isso vamos partir para o somatório das forças em :
Como o carregamento é simétrico então ambas as reações são iguais:
Passo 3
Novamente pelo fato do carregamento ser simétrico vamos ter que o momento fletor máximo ocorre exatamente no meio:
Passo 4
Agora vamos achar o momento resistente mínimo que a viga deve possuir , que é dado por:
Passo 5
Agora vamos escolher a viga com e a mais econômica, com a menor altura. Temos de fazer isso comparando com a tabela no final no livro. Assim vamos ter o perfil:
Passo 6
Agora para responder à letra vamos analisar a longarina:
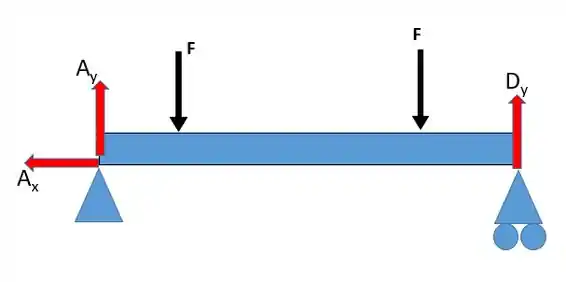
Aqui temos de notar que as forças são iguais à soma do carregamento distribuído de cada dupla de vigas, assim:
Lembrando que não existem forças em podemos fazer o somatório das forças em :
Como o carregamento é simétrico:
Passo 7
Novamente pelo fato do carregamento ser simétrico vamos ter que o momento fletor máximo ocorre exatamente no meio:
Passo 8
Agora vamos achar o momento resistente mínimo que a viga deve possuir , que é dado por:
Passo 9
Agora vamos escolher a viga com e a mais econômica, com a menor altura. Temos de fazer isso comparando com a tabela no final no livro. Assim vamos ter o perfil:
Resposta
a)
b)