Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 7.Problemas - Ex. 21

A elevação da plataforma de massa m suportada pelos quatro elos idênticos é controlada pelos cilindros hidráulicos AB e AC que são articulados no ponto A. Determine a compressão P em cada um dos cilindros necessária para suportar a plataforma por um

Passo 1

Primeiro, vamos desenhar o diagrama de força ativa

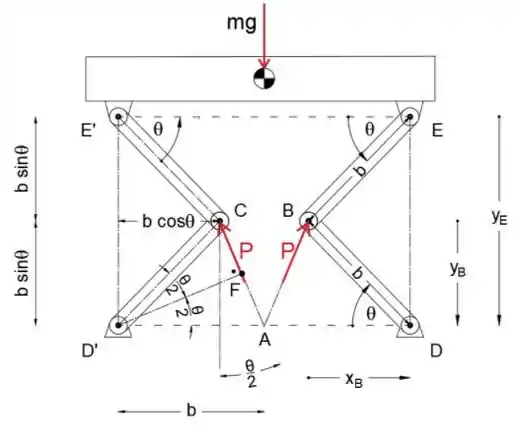
Olhando para o esboço, podemos ver que os movimentos virtuais xB, yB e yE são

x B = b c o s ⁡ θ y B = b s i n ⁡ θ y E = 2 b s i n ⁡ θ

Portanto, mudanças infinitesimais de posição são

δ x B = - b s i n ⁡ θ δ θ δ y B = b c o s ⁡ θ δ θ δ y E = 2 b c o s ⁡ θ δ θ

Olhando para o triângulo isósceles △ ADB podemos notar que a linha FD ^ 'faz com a horizontal o ângulo de θ / 2, já que FD' faz ângulo reto com a AC, podemos dizer que AC faz com a vertical o mesmo ângulo, ou seja, força P malas com o ângulo vertical de θ / 2

Passo 2

Observe que o ponto B se move em ambas as direções x e y, então o trabalho virtual feito pela força P é

δ U P = P x δ x B + P ∃ δ y B

Primeiro substituiremos P x e P y por P s i n ⁡ θ 2 e P c o s ⁡ θ 2

δ U P = P s i n ⁡ θ 2 δ x B + P c o s ⁡ θ 2 δ y B

Substituiremos x B e y B por - b s i n ⁡ θ δ θ e b c o s ⁡ θ δ θ

δ U P = - P s i n ⁡ θ 2 b s i n ⁡ θ δ θ + P c o s ⁡ θ 2 b c o s ⁡ θ δ θ δ U P = P b - s i n ⁡ θ 2 s i n ⁡ θ + c o s ⁡ θ 2 c o s ⁡ θ δ θ

Conhecendo c o s ⁡ ( α + β ) = c o s ⁡ α c o s ⁡ β - s i n ⁡ α s i n ⁡ β , podemos escrever a equação acima

δ U P = P b c o s ⁡ 3 2 θ δ θ (1)

Trabalho virtual realizado por peso mg é produto do peso e seu deslocamento vertical

δ U m g = m g δ y E

Substituiremos δ y E por 2 b c o s ⁡ θ δ θ

δ U mg  = 2 l m ⁡ g c o s ⁡ θ δ θ (2)

Passo 3

Ao aplicar o Princípio do Trabalho Virtual, observe que existem dois cilindros hidráulicos, ou seja, duas forças P

δ U = 0   2 δ U P + δ U m g = 0

Substituiremos δ U P e δ U m g pelas expressões (1) e (2), respectivamente

2 P b c o s ⁡ 3 2 θ δ θ + 2 b m g c o s ⁡ θ δ θ = 0   / ⋅ 1 2 b δ θ

Dividiremos ambos lados da equação por 26 θ ¨

P c o s ⁡ 3 2 θ + m g c o s ⁡ θ = 0

Por fim, escreveremos P como

P = m g c o s ⁡ θ c o s ⁡ 3 2 θ

Resposta

P = m g c o s ⁡ θ cos ⁡ 3 2 θ

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

No mecanismo mostrado, a mola de rigidez k é descomprimida quando θ = 60 ∘. Além disso, as massas das peças são pequenas em comparação com a soma das massas dos dois cilindros. O mecanismo é construíd
Os rolos de extremidade da barra AB uniforme de 20 lb movem-se livremente nas guias horizontal e vertical, conforme mostrado. Determine o valor mais baixo da posição de equilíbrio θ sob a ação de 480-
Determine o ângulo de equilíbrio θ para o mecanismo mostrado. A mola de rigidez k = 12 lb / in. tem um comprimento não esticado de 8 pol. Cada um dos elos uniformes AB e CD tem um peso de 10 lb, e o m
Um eixo de aço de 2,5 m de comprimento e 30 mm de diâmetro gira a uma frequência de 30 Hz. Determine a potência máxima que o eixo pode transmitir, sabendo que G=77,2 GPa, que a tensão de cisalhamento
O alçapão uniforme de 25 kg é livremente articulado ao longo de sua borda inferior O-O e é preso às duas molas, cada uma com rigidez k = 800 N / m. As molas não são alongadas quando θ = 90 ∘. Tome V_g