Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 7.Problemas - Ex. 75
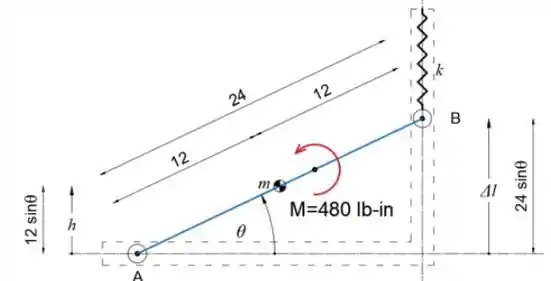
Os rolos de extremidade da barra AB uniforme de 20 lb movem-se livremente nas guias horizontal e vertical, conforme mostrado. Determine o valor mais baixo da posição de equilíbrio θ sob a ação de 480-lb-pol. par M e a mola de rigidez k = 1,25 lb / in. A mola é descomprimida quando θ = 0
Passo 1
Primeiro, vamos desenhar o diagrama de força ativa
Uma vez que existe o par M atuando no sistema, uma mola está ligada e a massa do sistema é m, podemos escrever a equação de equilíbrio como
(1)
Podemos ver a partir do esboço que a altura do centro de massa é
Embora a mudança no comprimento da primavera seja
Passo 2
Trabalho virtual feito pelo par M é igual ao produto do momento M e mudança na rotação δα
Substituiremos por 480 lb-in
(2)
Uma vez que a mudança no comprimento da mola é Δl, podemos escrever a expressão para a energia potencial elástica como
Substituiremos por e by in
Derivaremos ambos lados da equação
(3)
Passo 3
Podemos ver que a massa de m atua na altura h, então a expressão para energia potencial gravitacional é
Substituiremos por e by
Derivaremos ambos lados da equação
(4)
Finalmente, vamos substituir δUF, δVe e δVg pelas expressões (2), (3) e (4) na equação de equilíbrio (1)
(5)
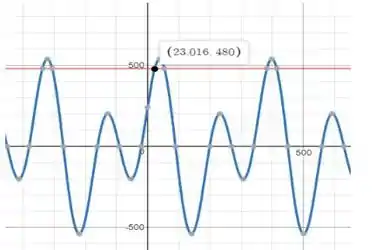
Usando uma calculadora gráfica como o Desmos (link nos comentários), traçaremos a função 720sinsθcosθ + 240cosθ e leremos o menor ângulo θ para o qual a função
tem um valor de 480
Podemos ver no gráfico que o menor ângulo em que o sistema está em equilíbrio é
