Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 7.Problemas - Ex. 58

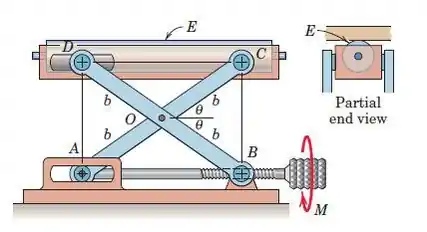
O suporte portátil de rolos para apoiar as placas ejetadas de uma plaina de madeira é projetado com um ajuste de altura microfino produzido girando o botão serrilhado do parafuso de ajuste com um torque M. O parafuso de rosca única com roscas quadradas tem um passo p (avanço por rotação ) e é rosqueado no colar em B para controlar a distância entre A e B (e, portanto, C e D). O rolo E e a caixa de suporte têm uma massa m_1, e os quatro elos uniformes (dois de cada lado) têm uma massa combinada m_2 e um comprimento 2b para cada um. Despreze todo o atrito e encontre o torque M necessário para elevar o rolo para um determinado valor de θ.

Passo 1

O enunciado pede que a gente Despreze todo o atrito e encontre o torque M necessário para elevar o rolo para um determinado valor de θ.

Como há um par M agindo no sistema, que contém as massas m_0 e m, podemos escrever a equação de equilíbrio ns

δ U = δ V δ U M = δ V g

Podemos ver no esboço que as alturas h1 e h2 são

h 1 = 2 b s i n ⁡ β h 2 = b s i n ⁡ θ

Também podemos ver no esboço que o Movimento Virtual do ponto B é

x = 2 b c o s ⁡ θ

Passo 2

Observe que podemos escrever esta distância como função do ângulo α também

Sabemos que o parafuso é de rosca única, portanto, o ângulo de 2π é necessário para que o ponto B se mova a distância p, a distância é igual ao produto do ângulo e razão p 2 π

x = α p 2 π

Uma vez que escrevemos distância x em função de α e θ, podemos determinar a relação entre esses dois ângulos

α P 2 π = 2 b c o s ⁡ θ α = 2 π p 2 b c o s ⁡ θ

Passo 3

Derivaremos ambos lados das equações

δ α = - 4 b π p s i n ⁡ θ

Passo 4

O Trabalho Virtual realizado pelo par M é produto da Rotação Virtual δα e do momento que a força produz

δ U M = M δ α

Substituiremos δ α pela expressão - 4 b π p s i n ⁡ θ

δ U M = - M 4 b π p s i n ⁡ θ δ θ

uma vez que existem duas massas no sistema, ambas indo para baixo, podemos escrever a expressão para a energia potencial gravitacional como-

V g = - m 1 g h 1 - m 2 g h 2 V g = - g m 1 h 1 + m 2 h 2

Substituiremos h 1 por 2 b s i n ⁡ θ e h 2 por b s i n ⁡ θ

V g = - g 2 m 1 b s i n ⁡ θ + m 2 b s i n ⁡ θ V g = - g b s i n ⁡ θ 2 m 1 + m 2

Derivaremos ambos lados da equação

δ V g = - g b c o s ⁡ θ 2 m 1 + m 2 δ θ (3)

Passo 5

Por fim, substituiremos δ U M e δ V g pelas expressões (2) e (3) na equação(1), respectivamente

- M 4 b π p s i n ⁡ θ δ θ = - g b c o s ⁡ θ 2 m 1 + m 2 δ θ   / ⋅ - 1 b δ θ

Dividiremos ambos lados da equação por - b δ θ

M 4 π p s i n ⁡ θ = g c o s ⁡ θ 2 m 1 + m 2

Escreveremos as equações para ambas M como

M = g p 2 m 1 + m 2 4 π t a n ⁡ θ

Resposta

M = g p 2 m 1 + m 2 4 π t a n ⁡ θ

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O esboço mostra a configuração aproximada do projeto de um dos quatro conjuntos de retenção de ação alternada que prendem o flange da base de um veículo-foguete ao pedestal de sua plataforma antes do
O portão de garagem AB uniforme mostrado na seção tem uma massa m e está equipado com dois dos mecanismos carregados por mola mostrados, um em cada lado da porta. O braço OB tem massa desprezível e o
Um bloco retangular uniforme de altura he massa m é centrado em uma posição horizontal na superfície circular fixa de raio r. Determine o valor limite de h para estabilidade.
Um mecanismo de controle consiste em um eixo de entrada em A que é girado pela aplicação de um par M e um controle deslizante de saída B que se move na direção x contra a ação da força P. O mecanismo
Use o princípio do trabalho virtual para determinar o coeficiente mínimo de fricção μ_s entre a caixa de 40 kg e as garras das pinças de fricção simétricas para que a caixa não deslize. Resolva o caso