Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 7.Problemas - Ex. 79

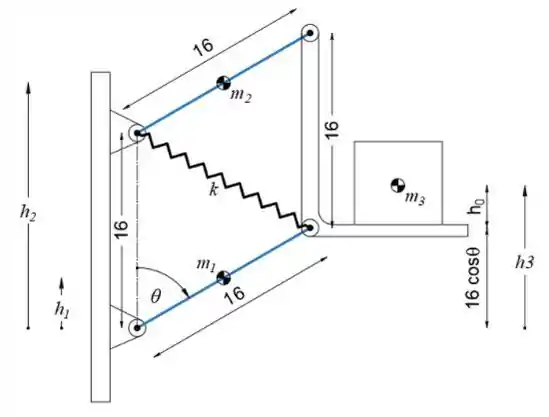
Determine o ângulo de equilíbrio θ para o mecanismo mostrado. A mola de rigidez k = 12 lb / in. tem um comprimento não esticado de 8 pol. Cada um dos elos uniformes AB e CD tem um peso de 10 lb, e o membro BD com sua carga pesa 100 lb. O movimento está no plano vertical.

Passo 1

Primeiro, vamos desenhar o diagrama de força ativa

Observe que não há forças externas atuando no sistema, portanto, podemos escrever a equação de equilíbrio como

δ V = 0 δ V e + δ V g = 0 (1)

Podemos determinar o comprimento da mola como no Problema 7/77

l = 32 s i n ⁡ θ 2

Sabendo que o comprimento da mola relaxada é l_0 = 8 pol. Podemos escrever a mudança no comprimento da mola como

Δ l = l - l 0 Δ l = 32 s i n ⁡ θ 2 - 8

Podemos ver a partir do desenho que as alturas dos centros de massa são

h 1 = 8 c o s ⁡ θ h 2 = 16 + 8 c o s ⁡ θ h 3 = 16 c o s ⁡ θ + h 0

Passo 2

Uma vez que o mecanismo contém três massas, podemos escrever a expressão para a energia potencial gravitacional como

V g = w 1 h 1 + w 2 h 2 + w 3 h 3

Substituiremos pesos por seus valores e alturas por expressões escritas na etapa anterior

V g = 10 ⋅ 8 c o s ⁡ θ + 10 ( 16 + 8 c o s ⁡ θ ) + 100 16 c o s ⁡ θ + h 0

Derivaremos ambos lados da equação

δ V g = ( - 80 s i n ⁡ θ - 80 s i n ⁡ θ - 1600 s i n ⁡ θ ) δ θ

δ V g = - 1760 s i n ⁡ θ δ θ (2)expressão para energia potencial elástica

V e = 1 2 k ( Δ l ) 2

Substituiremos k por 12 l b / i n e ( Δ l ) 2 by 32 s i n ⁡ θ 2 - 8 2

V e = 1 2 ⋅ 12 32 s i n ⁡ θ 2 - 8 2

Derivaremos ambos lados da equação

δ V e = 6 ⋅ 32 c o s ⁡ θ 2 32 s i n ⁡ θ 2 - 8 δ θ δ V e = 192 c o s ⁡ θ 2 32 s i n ⁡ θ 2 - 8 δ θ (3)

Passo 3

A seguir, substituiremos δVg e δVe pelas expressões (2) e (3) na equação (1)

- 1760 s i n ⁡ θ + 192 c o s ⁡ θ 2 32 s i n ⁡ θ 2 - 8 δ θ = 0

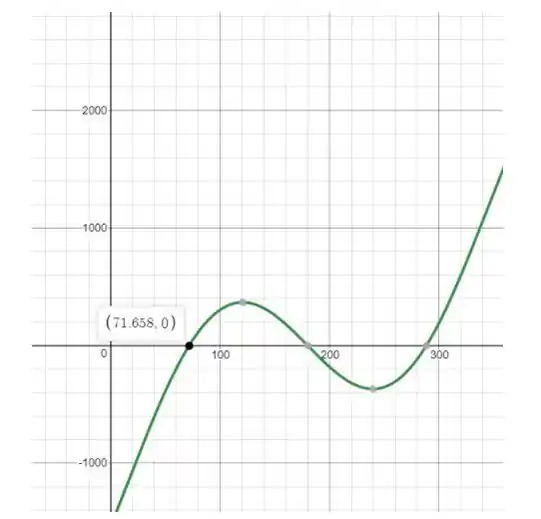
Usando Desmos, podemos ver o ângulo θ que satisfaz a equação acima,

ou seja, em que o sistema está em equilíbrio é

θ = 71.658 ∘  and  θ = 180 ∘

Resposta

θ = 71.658 ∘   e   θ = 180 ∘

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

75- A barra O A , que tem uma massa de 25k g e centro de massa em G , é articulada em torno de sua extremidade O e balança no plano vertical sob a restrição do contrapeso de 10k g . Escreva a expressã
77- A figura mostra a vista lateral de uma janela de ventilação de 10k g e centro de massa em G , articulada em relação a um eixo horizontal que passa por sua aresta em O . Quando θ = 90 , a mola de r
79- A conexão uniforme O A tem uma massa de 20k g e está apoiada no plano vertical pela mola A B cujo comprimento é de 400m m quando não está esticada. Faça um gráfico da energia potencial total V e d
78- O mecanismo articulado é usado para levantar a massa de 80k g para uma posição travada quando O B se move para O B ' na posição a 3 ° . Para avaliar a ação projetado do mecanismo, faça um gráfico
80- Determine o ângulo de equilíbrio θ para o mecanismo mostrado. A mola de rigidez k = 2 k N / m tem um comprimento de 200m m quando não está esticada. Cada uma das conexões uniformes A B e C D tem u