Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 7.Problemas - Ex. 46
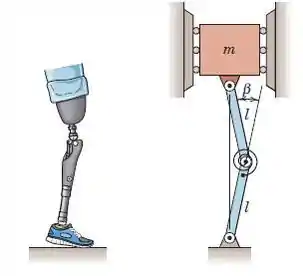
Um dos requisitos críticos no projeto de uma perna artificial para um amputado é evitar que a articulação do joelho dobre sob a carga quando a perna está esticada. Como uma primeira aproximação, simule a perna artificial pelos dois elos leves com uma mola de torção em sua junta comum. A mola desenvolve um torque M = Kβ, que é proporcional ao ângulo de curvatura β na junta. Determine o valor mínimo de K que garantirá a estabilidade da articulação do joelho para β = 0.
Passo 1
Primeiro, vamos desenhar o diagrama de força ativa
Observe que não há forças externas agindo, portanto, podemos escrever a equação de equilíbrio como
(1)
Podemos ver no esboço que a distância h é
Enquanto a deflexão angular da mola é β
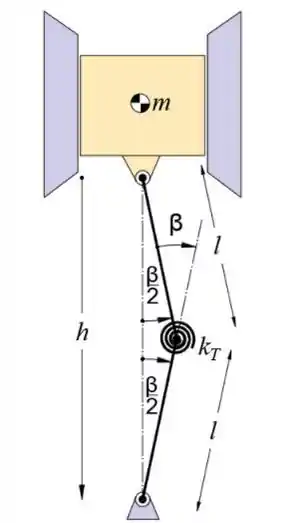
Passo 2
Expressão para energia potencial gravitacional
Substituiremos
Derivaremos ambos lados da equação
(2)
Passo 3
Expressão para energia potencial elástica
Derivar ambos lados da equação
(3)
Passo 4
A seguir, substituiremos δVg e δVe pelas expressões (2) e (3) na equação de equilíbrio (1)
Observe que o sistema é estável quando a segunda derivada da equação de equilíbrio é maior que zero
Para verificar a estabilidade da posição β = 0, vamos simplesmente colocar o valor de β em
Podemos ver que o valor mínimo de kT necessário para garantir a estabilidade é