Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 4.Problemas - Ex. 46
O elo rígido é sustentado por um pino em , um cabo de aço com comprimento de quando não alongado com área de seção transversal de e um bloco curto de alumínio com de comprimento quando não carregado com área de seção transversal de . Se o elo for submetido à carga vertical mostrada, determine a tensão normal média no cabo e no bloco. , .
Passo 1
Um elo em formato de “L” tem três suportes: um pino em , um cabo de aço e um bloco de alumínio em D (uma barra ligando o “L” a uma parede).
Características do cabo :
- Aço:
- Área transversal: .
- Comprimento inicial: .
- Alumínio: ,
- Área transversal: .
- Comprimento inicial: .
Características do bloco em :
O carregamento é uma força vertical concentrada de .
Tem suportes demais nesse elo, o papel deles é deixar o “L” fixo. Porém, quando o carregamento atuar, o “L” vai girar um pouco ao redor do pino em , então o cabo e o bloco vão deformar (esticando e comprimindo).
Queremos a tensão no cabo e no bloco, responsáveis por essas deformações.
Passo 2
Diagrama de corpo livre.
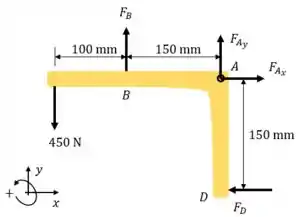
Agora checamos as condições de equilíbrio. Vamos fazer o equilíbrio dos momentos no ponto , assim as reações ali () não contribuem e não precisamos nos preocupar com esses caras. Atenção aos sinais!
Vamos precisar de mais uma equação.
Passo 3
A outra equação vem da condição de compatibilidade. O elo gira por causa do carregamento, e como ele é rígido, vai fazer o mesmo ângulo em todos os lugares.
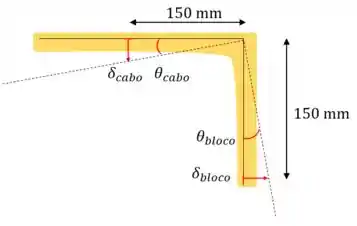
Tem que ter atenção a duas coisas aqui que acontecem porque estamos considerando pequenas deformações:
- Podemos considerar que as deformações no cabo e bloco foram retas
- É válido .
Nossa
Foi coincidência as distâncias serem iguais! Em outras questões parecidas, você tem que se preocupar com o ângulo primeiro!
Passo 4
Use a fórmula da relação carga-deslocamento
Coloque os valores para achar:
Substitua na equação que saiu do equilíbrio dos momentos:
Passo 5
Use a fórmula da tensão para acabar:
Resposta
Tensão normal no cabo: . Tensão normal no bloco: .