Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 4.Problemas - Ex. 5

A haste de aço A - 36 está sujeita ao carregamento mostrado. Se a área de seção transversal da haste for 60   m m 2 , determine o deslocamento de B e A . Despreze o tamanho dos acoplamentos em B ,   C   e   D .

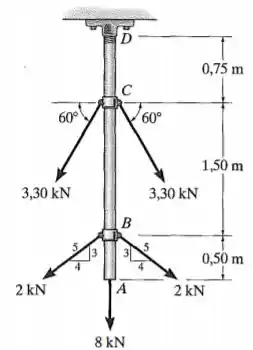
Passo 1

Como o material tratado no problema é o aço A - 36 temos que o módulo de elasticidade é tabelado e dado por E = 200 G P a . Além disso, podemos subdividir o problema em três pedaços onde calculamos o deslocamento da parte A B ,   B C e da parte C D separadamente e no final o deslocamento total servirá para encontrarmos o deslocamento de A ,   enquanto que o deslocamento de B C + C D vai nos dar o deslocamento de B . Para calcularmos esse deslocamento vertical vamos usar

δ = P ⋅ L A ⋅ E

Onde L é a extensão do segmento que estamos analisando.

Passo 2

δ a b = P a ⋅ L a b A a b ⋅ E = 8 k N ⋅ 0,5 m 60 m m 2 ⋅ 200 G P a

Para o segmento B C vamos fazer uma decomposição da força para pegarmos apenas a componente vertical que vai ser quem efetivamente vai nos importar. Assim

δ b c = P a + 2 P b ⋅ 3 5 ⋅ L b c A b c ⋅ E = ( 8 k N + 4 k N ⋅ 3 5 ) ⋅ 1 , 5 m 60 m m 2 ⋅ 200 G P a

Para o segmento C D também precisaremos fazer a decomposição da força para pegarmos apenas a componente vertical, dessa forma

δ c d = P a + 2 P b ⋅ 3 5 + 2 P c ⋅ s e n 60 ° ⋅ L c d A c d ⋅ E =

δ c d = ( 8 k N + 4 k N ⋅ 3 5 + 6,6 k N ⋅ s e n ( 60 ° ) ) ⋅ 0 , 7 5 m 60 m m 2 ⋅ 200 G P a

Agora,conseguimos, enfim, calcular o deslocamento vertical em B e em A fazendo

δ a = δ a b + δ b c + δ c d ≈ 2,641   m m

δ b = δ b c + δ c d ≈ 2,307   m m

Resposta

δ b = 2,307   m m   e   δ a = 2,641   m m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um suporte para tubos apoiado por molas é composto por duas molas que, na posição original, não estão alongadas e têm rigidez k = 60 k N / m , três hastes de aço inoxidável 304 ,A BeC D , com diâmetro
A carga é sustentada pelos quatro cabos de aço inoxidável 304 conectados aos elementos rígidos A B e D C . Determine o deslocamento vertical da carga de2,5k N se os elementos estiverem na horizontal q
A peça fundida é feita de um material com peso espedfico γ e módulo de elasticidade E . Se ela tiver a forma da pirilmide cujas dimensões são mostradas na figura, determine até que distância sua extre
Uma bola cujas extremidades foram truncadas é usada para suportar a carga de apoio P . Se o módulo de elasticidade para o material for E , determine o decréscimo em sua altura quando a carga é aplicad
Determine o alongamento da tira de alumínio quando submetida a uma força axial de 30k N .E a l=70G P a .