Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 16.Problemas - Ex. 91

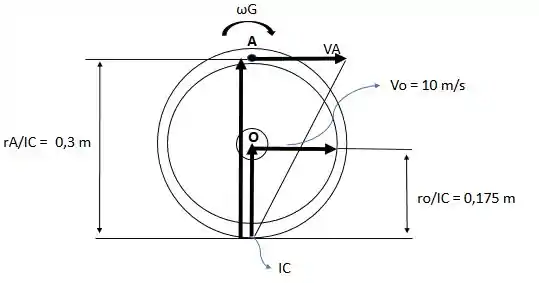
16.91. Se é dada uma velocidade ao centro da engrenagem, determine a velocidade do bloco deslizante no instante mostrado.

Passo 1

Movimento geral do plano: Como a cremalheira está estacionária, o da engrenagem está localizado no ponto de contato entre a engrenagem e a cremalheira, Fig. .

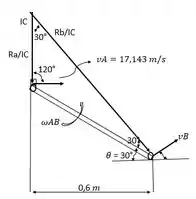
= 0,175 e = 0,6 . Assim, a velocidade do ponto pode ser determinada usando a semelhança entre triângulos mostrados na Fig.

Portanto:

= =

= 17, 143

(a)

Passo 2

A localização do segmento para a haste é indicada a partir da geometria mostrada na Fig. b.

Logo podemos determinar que:

Passo 3

Assim, a velocidade angular da engrenagem pode ser determinada a partir da relação entre a velocidade angular do segmento e a intersecção encontrada no ponto :

Passo 4

Visto que a velocidade angular nos segmentos é e = , podemos calcular a velocidade linear do ponto pela seguinte relação entre ambas:

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Quando um corpo submerso se move em um fluido, as partículas deste fluido circulam em torno do corpo e adquirem energia cinética. No caso de uma esfera movendo-se em um fluido ideal, a energia cinétic

duas hastes uniformes AB e CD, cada uma com comprimento l e massa m, são fixadas às engrenagens conforme mostrado. Sabendo que a massa da engrenagem C está dentro e que a massa da engrenagem A é de 4m

Quatro barras de mesma massa m e comprimento igual a l são conectadas por pinos em A, B, C e D e podem se mover em um plano horizontal. As barras são fixadas a quatro molas de mesma constante k e estã

Três hastes idênticas são conectadas conforme mostrado. Se b = 3 4 l , determine a frequência de pequenas oscilações do sistema.

Uma placa fina de comprimento l repousa sobre um semicilindro deraio r. Deduza uma expressão para o período de pequenas oscilaçõesda p.