Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 2.Problemas - Ex. 67
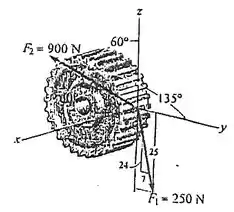
A engrenagem está submetida às duas forças caudadas pelo contato com outras engrenagens. Expresse cada força como um vetor cartesiano.
Passo 1
Vamos expressar cada força como um vetor cartesiano:
A está no plano então teremos duas componentes e encontraremos pela relação de catetos e hipotenusas do triângulo dado:
E o vetor cartesiano de fica:
Nossa direção é negativa de acordo com o sentido negativo da força em .
Passo 2
Já para nossa são dados dois ângulos de direção coordenados, vamos encontrar o terceiro pela relação:
Assim:
Passo 3
Agora vamos encontrar as componentes da usando os ângulos de direção:
Para :
Para :
E Para :
E o vetor cartesiano de fica:
Resposta
Exercícios de Livros Relacionados
172- Um sinal de trânsito está suspenso por dois cabos de 21m de comprimento, que têm uma massa de 1.2k g por metro. Determine a deflexão vertical δ do anel de junção A relativamente a sua posição ant
Duas forças atuam sobre o gancho. Determine a intensidade da projeção de F 2 ao longo de F 1 .
Determine a intensidade da componente projetada da força F a b que atua ao longo eixo z .
Determine as intensidades das componentes da força F = 600 N que atuam ao longo e perpendicular ao segmento D E do encanamento.
Dados os três vetores A ,BeD , mostre que A ⋅ B + D = A ⋅ B + ( A ⋅ D )