Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 15.Problemas - Ex. 72

Para as engrenagens mostradas na figura, deduza uma expressão para a velocidade angular ω C para a engrenagem C e mostre que ω C é independente do raio da engrenagem B. Considere que o ponto A é fixo e deduza a velocidade angular da barra ABC e a da engrenagem A por ω A B C e ω A respectivamente.

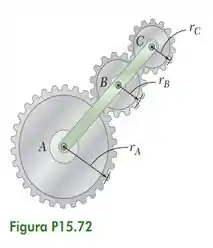
Passo 1

Questão 72 agora, meus chapas!

Bom! Pra começar vamos fazer um esboço do que mais ou menos está acontecendo em nosso problema... Um esboço das velocidades e dos vetores posição...

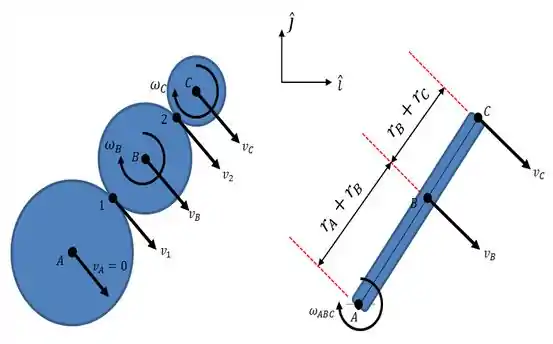
Passo 2

Se liga! Ao longo da barra A B C , a velocidade angular é dada por...

ω A B C = ω A B C

Como o ponto A é fixo, então...

v A = 0

E com base nas figuras esboçadas, temos que v B e v C serão dadas por...

v B = r A + r B ω A B C   ↘

v C = r A + 2 r B + r C ω A B C   ↘

Passo 3

A está fixo! Então, para a engrenagem maior, temos que...

ω A = 0

v A = 0

v 1 = 0

Já para a engrenagem B , uma vez que ela gira no sentido horário (com convenção negativa)...

v 1 = v B - r B ω B

Só que v 1 = 0 ...

v 1 = v B - r B ω B = 0

Logo, substituindo a relação que encontramos no P a s s o   2 ...

v B - r B ω B = 0

r A + r B ω A B C - r B ω B = 0

Isolando ω B :

r B ω B = r A + r B ω A B C

ω B = r A + r B r B ω A B C

Já a velocidade v 2 vai ser dada por...

v 2 = v B + r B ω B

Substituindo o v B do P a s s o   2 e o ω B que achamos anteriormente...

v 2 = v B + r B ω B

v 2 = r A + r B ω A B C + r B r A + r B r B ω A B C

v 2 = 2 r A + r B ω A B C   ↘

Passo 4

Para a engrenagem C , a gente tem que...

v 2 = v C - r C ω C

Substituindo o v 2 do P a s s o   3 e o v C do P a s s o   2 ...

v 2 = v C - r C ω C

2 r A + r B ω A B C = r A + 2 r B + r C ω A B C - r C ω C

r A - r C ω A B C = - r C ω C

Isolando ω C :

ω C = - r A r C - 1 ω A B C

ω C = 1 - r A r C ω A B C

Obtemos uma fórmula que depende apenas da velocidade angular da terceira engrenagem, de r A e r C . Viu só!? Nada de r B aqui!

Resposta

ω C = 1 - r A r C ω A B C

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

15.53. O braço ACB gira em torno do ponto C com velocidade angular de 40 rad /s no sentido anti-horário. Dois discos de atrito A e B estão presos por pinos em seus centros ao braço ACB do modo mostrad
15.55. Sabendo que a manivela AB tem uma velocidade angular constante de 160 rpm no sentido anti-horário, determine a velocidade angular da barra BD e a velocidade do colar D quando (a) 0, (b) 90°.
15.57. No sistema biela-manivela de motor mostrado na figura, l 160 mm e b 60 mm. Sabendo que a manivela AB gira com uma velocidade angular constante de 1.000 rpm no sentido horário, determine a veloc
15.56. Sabendo que a manivela AB tem uma velocidade angular constante de 160 rpm no sentido anti-horário, determine a velocidade angular da barra BD e a velocidade do colar D quando (a) 60°.
15.61. Uma cremalheira reta repousa sobre uma engrenagem de raio r 60 mm e está presa ao bloco B como mostra a figura. Sabendo que nesse instante a velocidade do bloco B é de 200 mm/s para a direita e