Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 8.Problemas - Ex. 21
Uma escada AB de 6,5 m encosta-se em uma parede como mostrado na figura. Considerando que o coeficiente de atrito estático é zero em B, determine o menor valor de em A para que o equilíbrio seja mantido.
Passo 1
Beleza! Vamos começar esse excercício desenhando o DCL para a escada, lembrando que a linha de reação entre o solo e a escada passa pelo ponto onde a força de apoio B e o peso se interceptam, sendo assim:
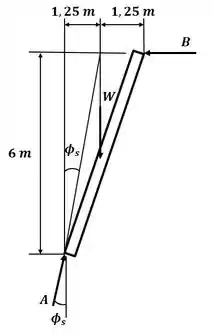
Passo 2
Agora ficou fácil, como vimos nessa seção, o coeficiente de atrito pode ser calculado como:
E, através do DCL do passo 1, temos:
Dessa forma, o coeficiente de atrito será:
Resposta
Exercícios de Livros Relacionados
O poste fino tem peso de 150 N e um comprimento de 7,8 m. Se ele for colocado na distancia d = 3, ele permanecerá nessa posição quando for solto ? O coeficiente de atrito estático entre o piso e o pos
O poste fino tem peso de 150 N e um comprimento de 7,8 m. Determine a distancia máxima d que ele pode ser colocado a partir da parede lisa sem escorregar. O coeficiente de atrito estático entre o piso
A escada uniforme de 10kg se apoia no piso rugoso para o qual o coeficiente de atrito estático é μ = 0 , 4 e contra a parede lisa em B. Determine a força horizontal P que o homem deve exercer na escad
A escada uniforme de 10kg se apoia no piso rugoso para o qual o coeficiente de atrito estático é μ = 0,8 e contra a parede lisa em B. Determine a força horizontal P que o homem deve exercer na escada
123- Calcule o torque M que o motor da caminhonete deve fornecer ao eixo traseiro para fazer com que as rodas dianteiras subam no degrau a partir de uma posição de repouso, sem que as rodas traseiras