Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 8.Problemas - Ex. 8
O poste fino tem peso de 150 N e um comprimento de 7,8 m. Determine a distancia máxima d que ele pode ser colocado a partir da parede lisa sem escorregar. O coeficiente de atrito estático entre o piso e o poste é de
Passo 1
TEMOS uma questão ótima de atrito. Porque ela vai conseguir reunir tudo o que a gente vem trabalhando de estática ate então .
Vamos fazer o diagrama de forças para identificar o que esta acontecendo nesse problema
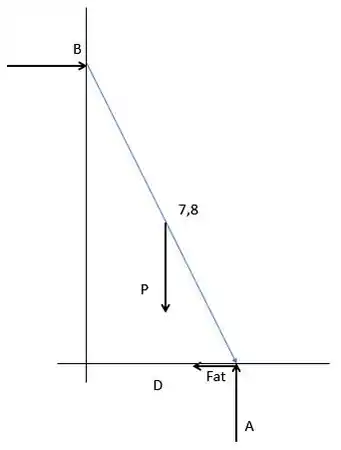
Passo 2
Vamos relembrar umas coisas. Estamos em estática. Então isso quer dizer que temos que satisfazer essas equações
Isso quer dizer que
Show. Temos todos esses dados. E para relacionar isso tudo vamos fazer o momento binário e ver o máximo de distancia que D pode assumir. Vamos escolher o ponto A. Assim matamos duas forças no momento. (Fat e A).
Vamos definir uma Orientação antes de começar. Gosto sempre de trabalhar em sentido horário. Essa orientação é arbitrária, se você estiver feito no sentido contrário, beleza! Só ao conferir as contas os sinais estarão trocados.
Então vamos lá. Tudo o que fizer meu sistema tentar rodar em Horário é ( + ), tudo o que tentar fazer tentar rodar em sentido contrário é ( - ) .
Outra coisa. Quando fazemos momento Binário temos que olhar para o PAR distância e força. Elas têm que ser ortogonais. Isso quer dizer que se uma força é horizontal ela faz par com distância na vertical. E vice-versa. Show! Vamos cair dentro.
Passo 3
Onde h é a altura que esse poste chega. Podemos achar ele por Pitagoras.
Pronto. 😊 Agora podemos concluir nosso calculo
Para resolvermos isso vamos elevar os dois lados ao quadrado
Show. Conseguimos achar o máximo que esse poste fica parado. Vamos para a próxima questão agora : )