Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 8.Problemas - Ex. 10
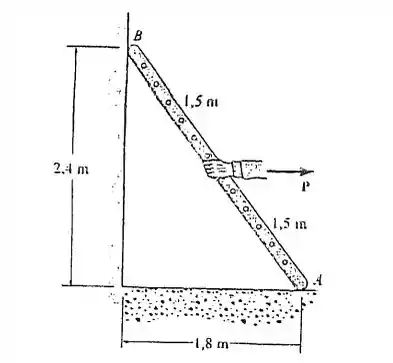
A escada uniforme de 10kg se apoia no piso rugoso para o qual o coeficiente de atrito estático é e contra a parede lisa em B. Determine a força horizontal P que o homem deve exercer na escada a fim de fazer com que ela se mova
Passo 1
Fala, querido! Então, aqui temos uma escada que sofre atrito do chão e um moço vai tentar mover essa escada para a direita. A pergunta é que força esse jovem precisa fazer para isso.
Vamos fazer o diagrama de forças para identificar o que está acontecendo nesse problema
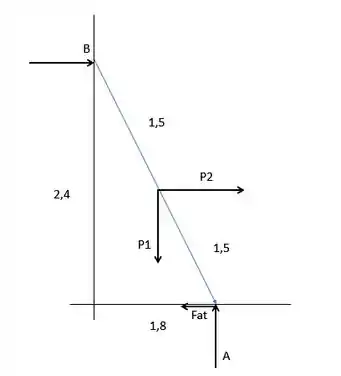
Vemos que não há reações verticais na parede porque ela é lisa, aí só temos reações horizontais.
Percebe também que a gente quer tirar a escada do repouso (move-la), para isso, a gente precisa vencer a força de atrito estático máxima, que é dada por
Onde é a força normal nesse ponto e é o coeficiente de atrito estático.
Com tudo isso em mente, a gente pode usar as equações de equilíbrio para achar . Bora!
Passo 2
Podemos usar umas equações de estática para saber o que está acontecendo aqui
Isso quer dizer que
Lembra que a gente precisa multiplicar a massa da escada pela gravidade. Como o a massa é , . Voltando para relação anterior que achamos
Percebe que a força normal no ponto é a reação no ponto , que a gente já achou. E percebe que o enunciado nos deu . Usando a fórmulinha para a força de atrito:
Passo 3
Agora, cara, a gente quer né. Percebe que a gente tem todas as forças menos e . Então para achar a que queremos, a gente pode calcular o somatório de momentos em relação a . Aí nosso resultado sai de cara.
Vamos considerar o sentido anti-horário positivo. Lembrando que o par distância e força precisam ser perpendiculares para calcularmos o momento causado pela força.
Substituindo os dados que a gente já achou
Isolando :
Ficou diferente do gabarito do livro, mas estamos certinhos!