Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 7.Problemas - Ex. 50

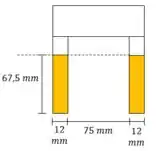
A escora é construída com três peças de plástico coladas como mostra a figura. Se a tensão de cisalhamento admissível para o plástico for τ a d m = 5,6   M P a e cada junta colada puder resistir a 50   k N / m , determine o maior carregamento distribuído w que pode ser aplicado agora

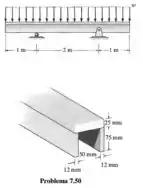
Passo 1

Dados da questão: L = 4 m ,   τ a d m = 5,6   M P a ,   q c o l a = 50 k N m

A questão pede: O maior carregamento w = ?

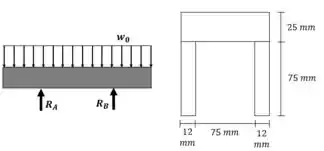
Estratégia de resolução: Primeiro vamos calcular as reações de apoio e os esforços internos na viga. Depois calculamos as propriedades geométricas da seção transversal: Centroide e Momento de Inércia.

O próximo passo será calcular o momento estático na cola e em seguida usamos a equação de fluxo de cisalhamento sobre a cola e determinamos o carregamento. (tendo atenção de que existem duas zonas coladas)

Por fim, calculamos o momento estático máximo da seção, e usamos a equação de tensão de cisalhamento para calcular o carregamento.

Passo 2

Começamos com um diagrama de corpo livre:

Como o carregamento e reações são perfeitamente simétricos:

R A = R B

∑ F y = 0 ⇒ R A + R B - w 0 L

2 R A = 4 w 0

R A = 2 w 0

E com os valores da reação, podemos usar o método gráfico para rapidamente calcular os esforços internos:

Observe que o maior esforço interno é:

V = w 0 L / 4

Passo 3

Agora calculamos o centroide:

y c = 25 ⋅ 74 ⋅ 87,5 + 2 ⋅ 75 ⋅ 12 ⋅ 37,5 25 ⋅ 74 + 2 ⋅ 75 ⋅ 12

y c = 62,84   m m

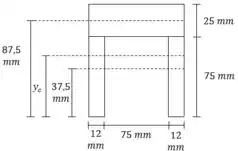
Passo 4

E calculamos o momento de inércia:

I v e r d e = 74 ⋅ 25 3 12 + 74 ⋅ 25 ⋅ 24,66 2 = 1,22 ⋅ 10 6   m m 4

I a m a r e l o = 2 12 ⋅ 75 3 12 + 12 ⋅ 75 ⋅ 25,34 2 = 2 ⋅ 10 6 m m 4

I = I a m a r e l o + I v e r d e = 3,22 ⋅ 10 6 m m 4

I = 3,22 ⋅ 10 - 6   m 4

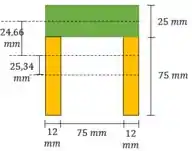
Passo 5

Agora vamos calcular o momento estático da cola. Em outras palavras, o momento estático da região verde:

Q = 75 ⋅ 24 ⋅ 25,34 = 45612   m m 3

Q = 45612 ⋅ 10 - 9   m 3

Passo 6

E agora calculamos o fluxo de cisalhamento que passa sobre a cola. Já temos o valor máximo q c o l a   que a cola pode resistir. Mas observe que temos duas regiões coladas, então o fluxo de cisalhamento q gerado pelo carregamento é dividido por dois.

q c o l a = q 2

Substituindo a equação do fluxo de cisalhamento

q c o l a = 1 2 ⋅ V Q I

Isolando o esforço interno

V = 2 q c o l a I Q

Substituindo o valor de V:

w 0 L 4 = 2 q c o l a I Q

Substituindo os valores:

w 0 ⋅ 4   m 4 = 2 ⋅ 50 k N m ⋅ 3,22 ⋅ 10 - 6 m 4   45612 ⋅ 10 - 9 m 3

w 0 = 7,06 k N m

Passo 7

Agora vamos calcular o momento estático para o cisalhamento máximo:

Q = 2 ⋅ 12 ⋅ 67,5 ⋅ 67,5 2

Q = 38216,77   m m 4

Q = 38216,77 ⋅ 10 - 9   m 4

Passo 8

Aplicamos a equação do cisalhamento:

τ a d m = V Q I ⋅ 2 t

Isolando V :

V = τ a d m ⋅ I ⋅ 2 t Q

Substituindo o valor de V

w 0 L 4 = τ a d m ⋅ I ⋅ 2 t Q

Substituindo os valores:

w 0 ⋅ 4 m 4 = 5,6 ⋅ 10 6 P a ⋅ 3,22 ⋅ 10 - 6 m 4 ⋅ 2 ⋅ 0,012   m 38216,77 ⋅ 10 - 9   m 3

w 0 = 11,32 k N m

Passo 9

O esforço máximo a ser resistido é o menor entre as duas opções, então:

w 0 = 7,06 k N m

Resposta

w 0 = 7,06 k N m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A viga foi construída com tábuas como mostra a figura. Se cada prego puder suportar uma força de cisalhamento de 1k N , determine o espaçamento máximo entre os pregos s, s’, s’’ com aproximação de 25
Determine a variação na altura d de uma em balanço que suporta uma força concentrada P em extremidade, de modo que ela tenha uma tensão de flexão máxima constante σ a d m em todo o seu comprimento. A
Trace os diagramas de força cortante e momento fletor para o eixo e determine, com aproximação de múltiplos de 5mm, o diâmetro exigido se σ a d m = 50M P a e τ a d m = 20 M P a . Os mancais em A e D e
Trace os diagramas de força cortante e momento fletor para o eixo e determine, com aproximação de múltiplos de 5mm, o diâmetro exigido se σ a d m = 50M P a e τ a d m = 20 M P a . Os mancais em A e D e
A viga mostrada na figura suporta uma força concentrada P e seu centro. Se for feita de uma chapa com largura constante b , determine a tensão de flexão máxima absoluta na viga